Um capacitor de placas paralelas de área está conectado a uma bateria cuja diferença de potencial é .
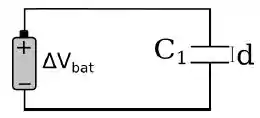
As placas do capacitor estão separadas por uma distância . Sem interromper as conexões, mãos isoladas separam um pouco mais as placas, sendo a nova distância entre elas igual a . A carga na situação inicial e a carga na situação final são, respectivamente.
e
e
e
e
e
Passo 1
A carga inicial no capacitor pode ser calculada da seguinte forma:
Para um capacitor de placas planas e paralelas, a capacitância é dada por:
Substituindo na expressão da carga:
Onde , logo:
Passo 2
Após afastarmos as placas do capacitor, a distância entre as mesmas passa a ser . Nessa configuração, a carga no capacitor passa a ser:
Agora é só arrumar a casa:
Resposta
e
Exercícios de Livros Relacionados
Os dois objetos de metal da Fig. 25-24 possuem cargas de + 70 pC e -70 pC, que resultam em uma diferença de potencial de 20 V. (a) Qual é a capacitância do sistema? (b) Se as cargas mudam para + 200 p
As placas de um capacitor de placas paralelas são separadas por uma distância d 0 e cada placa tem área A . Uma lâmina metálica d e área A é inserida entre as placas de maneira tal que a lâmina é para
Calcule:a) a capacitância de um par de placas paralelas com área de 100c m 2 cada, separadas de 3,0m m ;b) o campo elétrico quando o capacitor possui uma carga de 0,10μ C .
Um capacitor com placas paralelas no ar possui uma capacitância igual a 245 pF e um módulo de carga de 0,148 μ C em cada placa. A distância entre as placas é igual a 0,328 mm. (a) Qual é a diferença d
Na Figura 17.14, a chave comutadora está inicialmente na posição a . Calcule a carga Q 1 no capacitor de capacitância C 1 , após a chave ser comutada para a posição b e cessarem as correntes.