Um capacitor esférico é constituído por duas cascas esféricas metálicas concêntricas de raios a e b com a
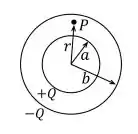
(a) (1,0 ponto) Calcule o vetor campo elétrico em um ponto P, localizado a uma distância r do centro geométrico do capacitor, tal que a
(b) (1,0 ponto) Calcule a diferença de potencial entre as placas do capacitor.
(c) (0,5 ponto) Calcule a capacitância deste capacitor.
Passo 1
Oiii gente! Vamos lá resolver essa questão. Mastigando o enunciado: é dado que um capacitor esférico constituído por duas cascas esféricas metálicas concêntricas de raios a e b com a
- Para descobrirmos a resposta desse item, temos que ver o que nos é pedido e o que é oferecido pela questão
- Para acharmos a diferença de potencial entre as placas, temos que nos lembrar qual sua fórmula, ou maneira que pode ser escrita que envolva a integral da área em questão, para que assim possamos desenvolver e chegarmos a resposta com as variáveis que nos foram fornecidas na questão.
- Para descobrirmos a capacitância, vamos partir do seu conceito para conseguirmos deduzir como é a fórmula que utilizaremos. Após isso, vamos aplicar os dados que foram fornecidos na questão e, se necessário, os que obtivemos.
Nesse caso, é pedido o campo elétrico em um ponto P a uma distância r. A imagem nos mostra uma representação de onde o ponto P pode estar dentro desse círculo.
“Não tô entendendo nada ”
Vou explicar de uma maneira melhor! Como a distância é radial, a área onde esse ponto P pode estar é um círculo. E essa informação é superimportante pra resolução, pois como o círculo é simétrico e estamos trabalhando com campo elétrico e com cargas, qual fórmula nos ajudará a descobrir o campo?
A lei de Gauss!! Isso mesmo, ela se aplica perfeitamente para casos em que o corpo carregado é simétrico (e queremos achar campo elétrico). Assim, temos:
Sendo a carga interna ao corpo, e a constante dielétrica.
Como apenas o que vai estar variando é a área, podemos tirar o campo elétrico de dentro da integral:
Como a área é a de um círculo, temos:
Substituindo a carga interna por Q e mudando a organização da equação, temos:
Sendo o raio do circulo.
Passo 2
A diferença de potencial é dada por:
Mas quem é e ?
nós já encontramos na letra A) e vai ser , pois apenas o raio está variando
Ao substituir, temos:
Tirando a parte que não varia para fora da integral, temos:
Vale lembrar que “” e ”” são os limites da integração porque são os valores máximo e mínimo do raio em questão
Passo 3
A capacitância é uma grandeza e ela mede a quantidade de armazenamento de energia e se relaciona com a diferença de potencial.
A fórmula a ser utilizada é
Sendo a capacitância, a carga e a variação de tensão!
Aí eu lhe questiono, temos os dados necessários para descobrir quem é ?
Temos sim!! Achamos nas letras anteriores. Então vamos substituir e chegarmos à resposta
Assim, temos a capacitância em função das variáveis da questão!!
Se ficou alguma dúvida, quer dar alguma sugestão ou reportar algum erro, manda um feedback pra gente! Vamos adorar ajudar você
Resposta
Item
Item
Item