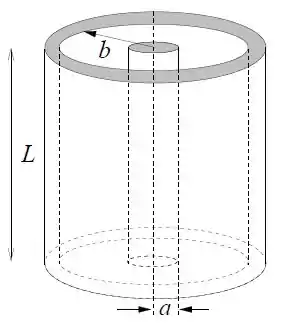
Um cilindro condutor de comprimento e raio , com carga , é coaxial a uma camada cilíndrica condutora maior, com raio interno e carga . Despreze efeitos de borda.
Calcule a capacitância do sistema.
Passo 1
Calcule a capacitância do sistema.
Se você nunca viu isso antes, pode parecer o tipo de coisa que você olha e fala: “Say whaaat?!”. Mas não tema, estamos aqui pra isso, não é nenhum bicho de sete cabeças.
Vamos seguindo o raciocínio lógico, ok?
Por definição, a capacitância é dada por:
Então temos que começar calculando o módulo do potencial .
Passo 2
Por definição:
Agora vamos voltar para a capacitância:
Resposta
Exercícios de Livros Relacionados
Os dois objetos de metal da Fig. 25-24 possuem cargas de + 70 pC e -70 pC, que resultam em uma diferença de potencial de 20 V. (a) Qual é a capacitância do sistema? (b) Se as cargas mudam para + 200 p
As placas de um capacitor de placas paralelas são separadas por uma distância d 0 e cada placa tem área A . Uma lâmina metálica d e área A é inserida entre as placas de maneira tal que a lâmina é para
Calcule:a) a capacitância de um par de placas paralelas com área de 100c m 2 cada, separadas de 3,0m m ;b) o campo elétrico quando o capacitor possui uma carga de 0,10μ C .
Um capacitor com placas paralelas no ar possui uma capacitância igual a 245 pF e um módulo de carga de 0,148 μ C em cada placa. A distância entre as placas é igual a 0,328 mm. (a) Qual é a diferença d
Na Figura 17.14, a chave comutadora está inicialmente na posição a . Calcule a carga Q 1 no capacitor de capacitância C 1 , após a chave ser comutada para a posição b e cessarem as correntes.