Lei de Gauss, Campo em Condutores, Capacitores e Dielétricos
Um cilindro condutor de comprimento e raio , com carga , é coaxial a uma camada cilíndrica condutora maior, com raio interno e carga . Despreze efeitos de borda.
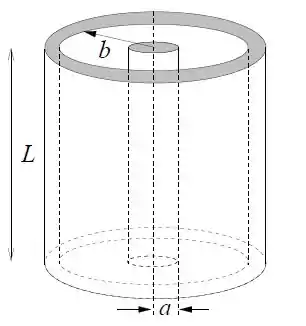
- Calcule o vetor campo elétrico na região .
- Calcule a capacitância do sistema.
- Qual é a energia eletrostática armazenada no sistema?
Passo 1
- Calcule o vetor campo elétrico na região .
- Calcule a capacitância do sistema.
- Qual é a energia eletrostática armazenada no sistema?
Poxa! Que lindo, não é verdade? Chegar no final da prova e, depois de quebrar a cabeça por mais de uma hora você encontra uma questão tranquila assim... então vamos aproveitar esse belo momento e matar essa aqui rápido, sem dó, nem piedade.
Pediu campo elétrico no condutor? Taca-lhe lei de Gauss!
Nesse caso, a nossa gaussiana será um cilindro de comprimento e raio , tal que .
A carga interna à nossa gaussiana será a carga do condutor de raio .
E a área da gaussiana será a área lateral do cilindro:
Feito isso, é só jogar na lei de Gauss e ser feliz!
Mas o problema pediu o vetor campo elétrico! Então, cuidado pra não dar mole.
O vetor campo elétrico aponta no sentido radial, logo:
Passo 2
Se você nunca viu isso antes, pode parecer o tipo de coisa que você olha e fala: “Say whaaat?!”. Mas não tema, estamos aqui pra isso, não é nenhum bicho de sete cabeças.
Vamos seguindo o raciocínio lógico, ok?
Por definição, a capacitância é dada por:
Então temos que começar calculando o módulo do potencial .
Passo 3
Por definição:
Agora vamos voltar para a capacitância:
Passo 4
A energia armazenada num capacitor é dada por:
Como já calculamos , basta substituir na equação acima:
Simples, certo? Você só precisa ter esses conceitos em mente e isso tende a ser um pouco mais tranquilo.