Lei de Gauss, Potencial Elétrico, Capacitores e Dielétricos
Um capacitor é formado por uma esfera condutora de raio e uma casca esférica condutora de raio , conforme a figura.
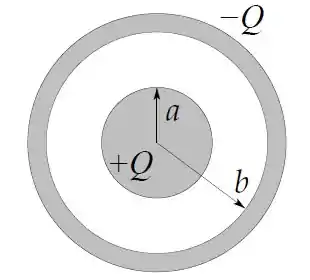
A esfera interna tem carga e a casca esférica tem carga . As respostas devem ser dadas apenas em termos de , , e .
Determine a diferença de potencial entre a esfera interna e a casca esférica.
Calcule a capacitância e determine a energia eletrostática armazenada no capacitor.
Passo 1
Determine a diferença de potencial entre a esfera interna e a casca esférica.
Pra calcular a diferença de potencial ente a esfera interna e a casca esférica, podemos começar calculando o campo elétrico através da Lei de Gauss e depois encontrando a diferença de potencial usando a equação:
A Lei de Gauss é dada por:
A partir da simetria esférica do problema, podemos simplificar a Lei de Gauss para:
Onde é a área da nossa gaussiana esférica:
Como estamos analisando a região entre a esfera interna e a casca esférica, . Assim, a carga que está dentro da nossa gaussiana é somente a carga da esfera.
Logo:
Passo 2
Agora que calculamos , podemos calcular a diferença de potencial:
Como , então , logo , ou seja, o potencial na esfera de raio é maior que o potencial da casca esférica, o que faz sentido, já que a esfera é carregada positivamente e a casca negativamente.
Passo 3
Calcule a capacitância e determine a energia eletrostática armazenada no capacitor.
Opa! Agora que acabamos de calcular a diferença de potencial, para calcular a capacitância, basta usar a equação:
Portanto:
Simplificando esse cara:
Passo 4
A energia armazenada em um capacitor é dada por:
Logo:
Opa! Mas o problema pediu para darmos as respostas em função de , , e ... isso significa que temos que sumir com esse .
é o campo elétrico na superfície da esfera interna de raio , dado por:
Isolando o , teremos:
Substituindo isso na nossa expressão de :
Simplificando esse cara, finalmente teremos:
Agora sim!
Resposta