Ache a superfície de ponto tais que a distância de ao ponto é a mesma do que a de ao plano .Identifique a superfície.
Passo 1
O problema não fala diretamente em quádricas nessa questão. Bom, primeiramente vamos encontrar a distância de ao ponto . Chamando essa distância de temos:
Passo 2
Perceba que a distância do ponto ao plano é compreendida como sendo a menor distância entre o ponto e o ponto mais próximo a ele, pertencente ao plano.
Ou seja, é a projeção do ponto no plano . Vamos chamar essa projeção do ponto no plano de .Perceba que . Geometricamente temos:
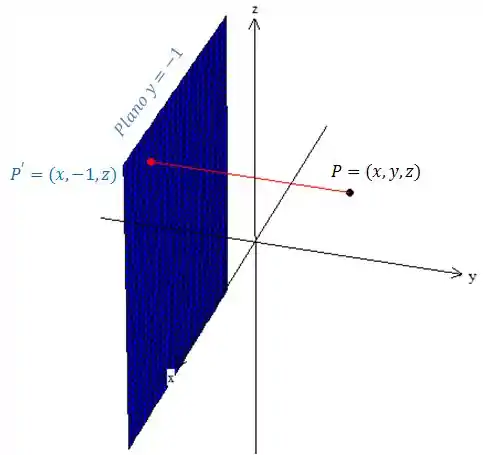
Passo 3
Como temos:
Que é a equação do paraboloide Elíptico
Resposta
Parabolóide Elíptico com equação: