Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cone e Parabolóides

Ver Teoria
Exercício 12345678910111213141516171819202122232425

Enunciado

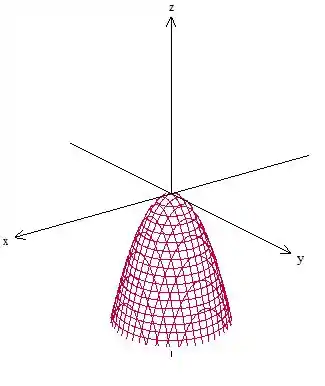
Esboce o gráfico da quádrica a seguir:

z = - ( x 2 + y 2 )

Passo 1

A quádrica apresentada no enunciado é um paraboloide elíptico, pois do lado esquerdo da equação tem uma variável “isolada” de grau 1 e do lado direito tem variáveis de grau 2 com sinais iguais.

Passo 2

Vamos fazer os traços:

Traços:

  • Traço no plano x y   z = 0 :

    • 0 = - ( x 2 + y 2 )

    Temos o ponto ( 0,0 , 0 )

  • Traço no plano x z   ( y = 0 ) :

    • z = - x 2

    Temos uma parábola. O traço fica:

  • Traço no plano y z   ( x = 0 ) :

    • z = - y 2

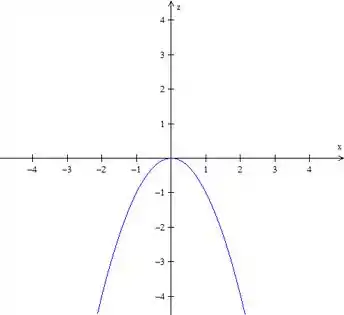
    Temos uma parábola. O traço fica:

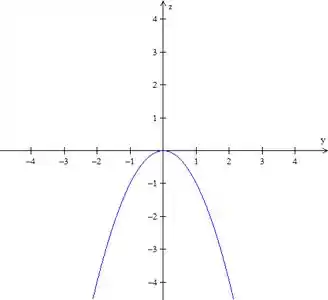
    Passo 4

    Vamos fazer agora interseções com planos paralelos aos eixos coordenados.

    Interseções:

  • Plano z = k

    • k = - ( x 2 + y 2 )

    Se k = 0 temos o ponto 0,0 , 0

    Se k ≠ 0 temos:

    1 = - x 2 + y 2 k

    Se k > 0 a equação acima é impossível. Logo não há interseção.

    Se k < 0 então a equação acima é um círculo.

    São elipses para k < 0

  • Plano y = k

    • z = - ( x 2 + k 2 )

    São Parábolas para k ∈ R  

  • Plano x = k

z = - ( k 2 + y 2 )

São Parábolas para k ∈ R  

Passo 3

Plote os traços que encontramos. Como as interseções da quádrica com eixos paralelos ao eixo z são elipses, para k < 0 , desenhe uma elipse na parte mais negativa do eixo z para demonstrar isso. O esboço fica:

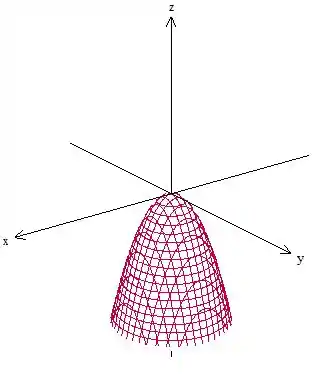
Resposta

Exercícios de Livros Relacionados

Os Exercícios 45-48 fornecem equações para parábolas e nos dize quantas unidades para cima ou para baixo e para direita ou para esquerda cada parábola deve ser deslocada. Encontre uma equação para a n
Os Exercícios 45-48 fornecem equações para parábolas e nos dize quantas unidades para cima ou para baixo e para direita ou para esquerda cada parábola deve ser deslocada. Encontre uma equação para a n
Os Exercícios 45-48 fornecem equações para parábolas e nos dize quantas unidades para cima ou para baixo e para direita ou para esquerda cada parábola deve ser deslocada. Encontre uma equação para a n
A parábola y2 = 8x é deslocada 2 unidades para baixo e 1 unidade para a direita para gerar a parábola (y + 2)2 = 8(x - 1). a. Encontre o vértice, foco e diretriz da nova parábola.b. Represente grafica
A parábola X2 = -4y é deslocada 1 unidades para esquerda e 3 unidade para cima para gerar a parábola (x+1)=4(y-3) a. Encontre o vértice, foco e diretriz da nova parábola.b. Represente graficamente os