Identifique essa Quádrica e faça seu esboço
Passo 1
Vamos fazer a superfície
Temos em
Porque coloquei tudo negativo dessa vez? O está negativo, então agora temos que por todo mundo negativo, se ele for positivo é como antes, sacou?
Então
Dessa forma devemos somar dos dois lados
Vamos ter em do lado esquerdo
Está lindão essa porra né? Só que não. O ideal é sempre termos a letra multiplicando então vamos por em evidência
Beleza?
Passo 2
Vamos para agora
Então
Dessa forma devemos somar dos dois lados
Vamos ter em do lado esquerdo
Beleza?
Passo 3
A equação vai ficar
Essa é uma equação de um cone, com eixo igual ao eixo , mas a ponta do coné não vai ser na origem vai ser no ponto
O gráfico vai ficar
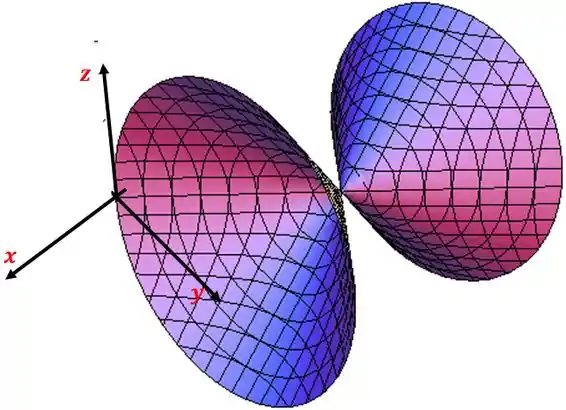
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Os Exercícios 45-48 fornecem equações para parábolas e nos dize quantas unidades para cima ou para baixo e para direita ou para esquerda cada parábola deve ser deslocada. Encontre uma equação para a n
Os Exercícios 45-48 fornecem equações para parábolas e nos dize quantas unidades para cima ou para baixo e para direita ou para esquerda cada parábola deve ser deslocada. Encontre uma equação para a n
Os Exercícios 45-48 fornecem equações para parábolas e nos dize quantas unidades para cima ou para baixo e para direita ou para esquerda cada parábola deve ser deslocada. Encontre uma equação para a n
A parábola y2 = 8x é deslocada 2 unidades para baixo e 1 unidade para a direita para gerar a parábola (y + 2)2 = 8(x - 1). a. Encontre o vértice, foco e diretriz da nova parábola.b. Represente grafica
A parábola X2 = -4y é deslocada 1 unidades para esquerda e 3 unidade para cima para gerar a parábola (x+1)=4(y-3) a. Encontre o vértice, foco e diretriz da nova parábola.b. Represente graficamente os