USP – Cálculo 2 – 2019 – P1 – Exercício 9
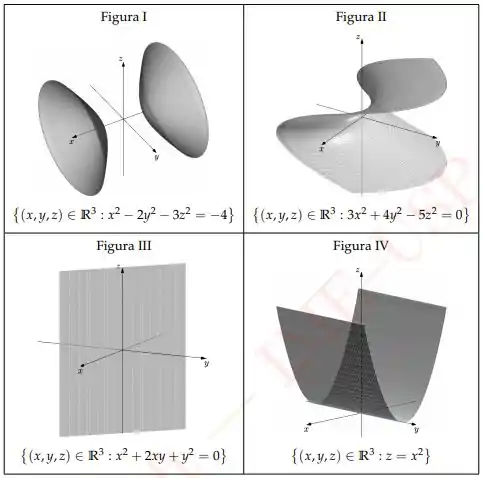
Dentre as figuras abaixo aquelas que associam corretamente e superfície são:
a) III e IV.
b) I e II.
c) I e III.
d) II e IV.
e) I e IV.
Passo 1
Legal, esse é um problema bem visual!
Temos que ver quais figuras a equação corresponde a superfície esboçada. Vamos olhar para a figura I com equação
Fazendo (para achar a interseção com o plano ), obtemos:
Trata-se de uma hipérbole com eixo real na direção . Mas note que na figura, a interseção da superfície com o plano é uma hipérbole com eixo real na direção . Já podemos descartar essa figura...
Passo 2
Na figura II, temos
Isolando :
Assim,
Trata-se de um cone, o que não corresponde a figura ☹
Passo 3
Na figura III, temos
Portanto,
Trata-se de um plano que corta a origem, exatamente como mostrado na figura. Guarde essa afirmativa!
Passo 4
Na figura IV, temos , que se trata de um cilindro parabólico. As interseções com planos são parábolas. A figura corresponde exatamente a isso 😊
Portanto, as figuras que a correspondência tá certa são III e IV. Alternativa A!
Resposta
Alternativa A.