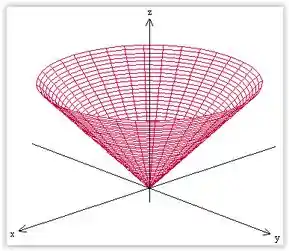
Faça um esboço da superfície, destacando as curvas de interseção com os planos coordenados , e .
Passo 1
Identificar a superfície:
Essa é a equação de um cone circular.
Mas como , então o gráfico dessa superfície é apenas a parte superior do cone:
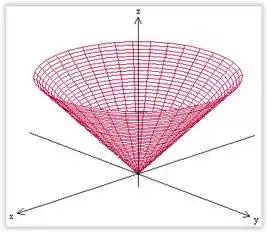
→ → Retas
→ → Retas
→ → Ponto
Resposta
Exercícios de Livros Relacionados
Os Exercícios 45-48 fornecem equações para parábolas e nos dize quantas unidades para cima ou para baixo e para direita ou para esquerda cada parábola deve ser deslocada. Encontre uma equação para a n
Os Exercícios 45-48 fornecem equações para parábolas e nos dize quantas unidades para cima ou para baixo e para direita ou para esquerda cada parábola deve ser deslocada. Encontre uma equação para a n
Os Exercícios 45-48 fornecem equações para parábolas e nos dize quantas unidades para cima ou para baixo e para direita ou para esquerda cada parábola deve ser deslocada. Encontre uma equação para a n
A parábola y2 = 8x é deslocada 2 unidades para baixo e 1 unidade para a direita para gerar a parábola (y + 2)2 = 8(x - 1). a. Encontre o vértice, foco e diretriz da nova parábola.b. Represente grafica
A parábola X2 = -4y é deslocada 1 unidades para esquerda e 3 unidade para cima para gerar a parábola (x+1)=4(y-3) a. Encontre o vértice, foco e diretriz da nova parábola.b. Represente graficamente os