UFMG – Cálculo 2 – P2 – Questão 4
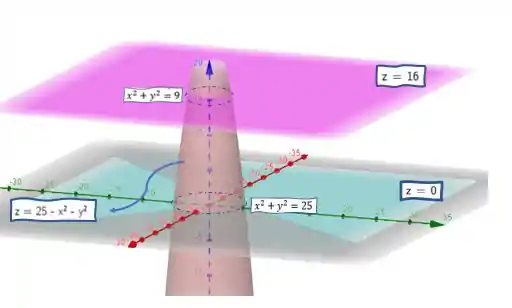
Esboce o gráfico de
Restrito à região a partir da interseção com os planos e
Passo 1
Oi, tudo bem? Essa questão parece complicada, mas vou ajudar você aqui! Vamos lá?
O problema nos deu uma superfície:
(ela não aprece uma parábola com boca para baixo em três dimensões? Pois é... a cara é a mesma! Chamamos essa superfície de paraboloide)
Mas para esboçar um gráfico não basta só olhar a ‘cara’ da superfície... precisamos ter uma noção das curvas que essa superfície faz ao interceptar os planos!
Os planos dados são:
Esses são planos “horizontais” se pensarmos em um sistema de coordenadas como estamos acostumados: e sendo ‘o chão’ e a ‘altura’.
Então é como se a gente “cortasse” em duas alturas esse paraboloide!
Temos também
Que é o plano , é como se fosse uma ‘parede’ lateral e
Que representa o plano : essa aqui é a ‘parede’ do fundo
A ideia para esboçar essa superfície é a seguinte: para cada plano dado, substituir na equação da superfície e determinar a curva que representa nesse plano
Com isso, achar a curva no plano correspondente.
E ir fazendo isso com todos os planos dados. Depois, com a ajuda de um programa que gera superfícies, juntar todas essas informações e desenhar a parte do paraboloide bem bonito!
Beleza?
Vamos começar?
Passo 2
Vamos começar desenhando os planos e .
Para (esse será nosso ‘chão’, já que representa o plano ) a superfície fica assim:
Essa curva representa um círculo de raio , e seu esboço é assim:
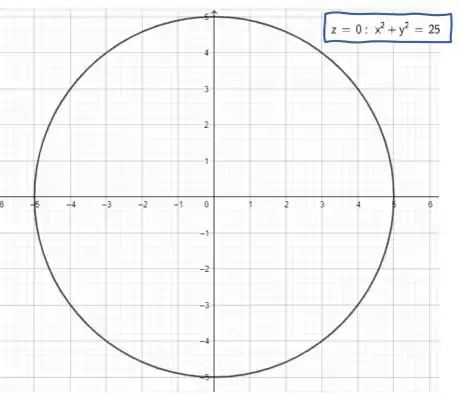
Beleza? E para , como será que fica?
Temos um outro círculo, mas agora de raio !
Isso quer dizer que bem no ‘chão’, o círculo é mais largo, enquanto na altura o círculo ‘afina’ para o raio . O esboço desse círculo é
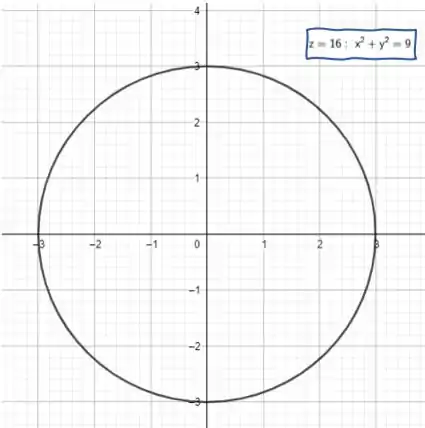
Tranquilo?
Vamos para os outros planos?
Passo 3
Agora precisamos ver a cara dessa superfície nos planos que formam as paredes laterais!
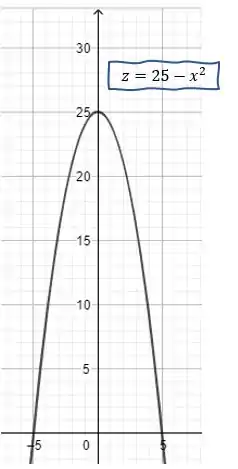
Primeiro com :
Opa! Isso é uma parábola com boca para baixo!
Essa parábola é a intersecção da superfície com a parede lateral esquerda! Pensa que em , ou seja, todo eixo , temos uma parábola com boca para baixo, batendo no em , como se fosse um arco-íris, que fofinho né?
O esboço dessa curva é:
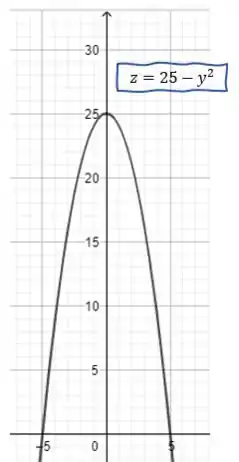
E agora, o último plano é o , jogando esse valor na superfície temos:
Você notou a semelhança? Pois é! Essa curva é bem parecida com a que encontramos no plano ! Isso porque o paraboloide é simétrico, e como temos os planos ordenados, a curva tem a mesma cara!
O esboço dessa aqui é:
Beleza?
Agora vamos reunir todas essas informações? Bora lá!
Passo 4
Nos cortes horizontais temos dois círculos, e nas paredes (lateral esquerda e fundo) uma parábola de boca para baixo que corta em e . Então reunindo todas essas características essa superfície fica assim:
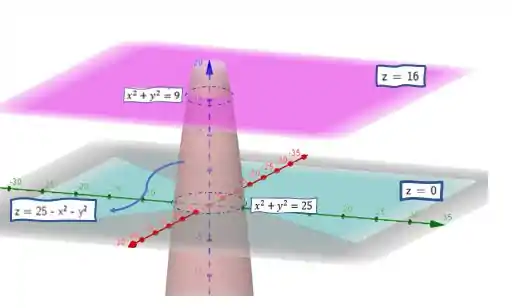É como se fosse um sorvete arredondado, de cabeça para baixo, cortado na ponta.
Ufa! Terminamos!
Espero ter ajudado!
Bora para próxima?
Resposta
