Determine uma equação da superfície obtida pela rotação da “parábola” em torno do eixo .
Passo 1
Oi, tudo bem? Essa questão parece complicada, mas vou ajudar e resolver passo a passo com você!
Vamos primeiro fazer um gráfico em para entender melhor o desenho:
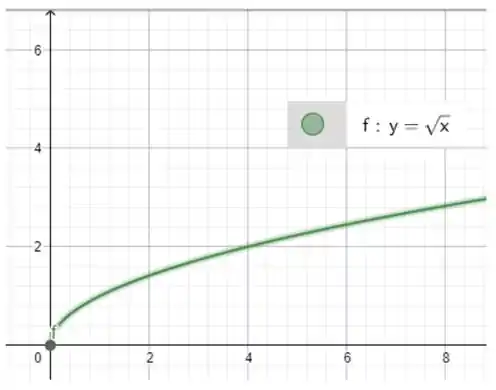
Então, temos que pensar agora que se rotacionarmos em torno do eixo , vamos ter um cone deitado, onde a figura formada pela secção reta vertical vai resultar em um círculo no plano .
A ideia é tentar desenhar em essa superfície e comparar com as equações dadas para ver qual é a equação que é resultado dessa rotação
Mas calma, vou fazer passo a passo com você!
Passo 2
Como falei ali no passo anterior, temos uma rotação da metade da parábola (parábola no eixo ) em relação ao eixo . Como a superfície é uma rotação, nos planos que não envolvem o eixo de rotação (no nosso caso o plano ), será formado um círculo

E a equação padrão de um círculo é com a variável ao quadrado, então se temos um círculo no plano , a equação dessa superfície deve ter .
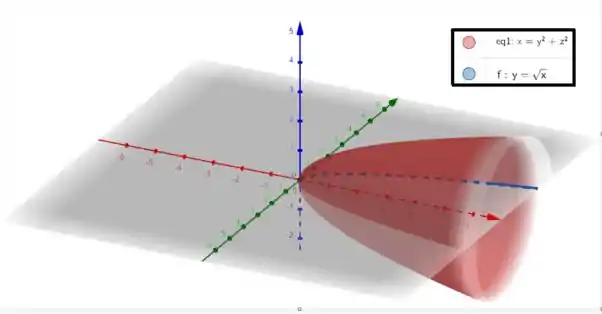
Então essa é a equação da nossa superfície!
Com a potência de igual a e a potência do e igual a 2.
Em azul está pontilhado a equação , e em vermelho o resultado da rotação em torno do eixo .
Beleza?
Sendo assim, a resposta correta é (c). E é isso! Espero ter ajudado!