Associe cada quádrica ao gráfico que mais se assemelha a ela:
Passo 1
Primeiramente devemos observar o grau de cada variável e os sinais dos coeficientes que estão multiplicando-as.
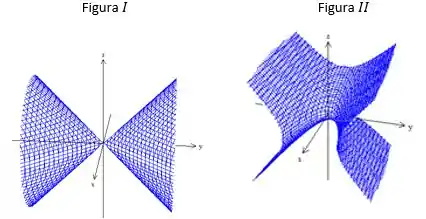
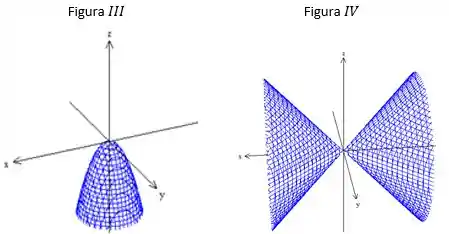
já está na forma padrão da equação do cone circular. Repare que o eixo do cone é o eixo pois é essa variável que está “isolada” na equação do cone. Portanto a melhor figura é a iv)
Passo 2
já está na forma padrão da equação do paraboloide hiperbólico(sela) pois temos uma variável com grau 1 de um lado da equação e do outro temos variáveis de grau 2 com sinais opostos.
Além disso, o eixo de grau 1 é o eixo , imagine que se uma pessoa fosse montar nessa sela, seu corpo ficaria paralelo ao eixo , e as pernas da pessoa ficariam ao longo do eixo com sinal negativo, eixo . Portanto, figura ii)
Passo 3
já está na forma padrão da equação do paraboloide elíptico, pois temos uma variável com grau 1 de um lado da equação e do outro temos variáveis de grau 2 com sinais iguais.
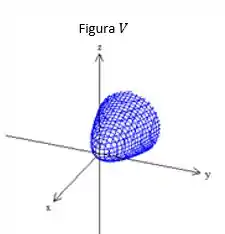
O eixo do paraboloide será o eixo (variável de grau 1) , pegando a porção negativa, devido aos sinais negativos da equação. Figura v)
Passo 4
Agora está na forma padrão da equação do paraboloide elíptico, pois temos uma variável com grau 1 de um lado da equação e do outro temos variáveis de grau 2 com sinais iguais.
O eixo do paraboloide será o eixo (variável de grau 1) , pegando a porção negativa devido aos sinais negativos da equação. Figura iii)
Passo 5
Agora está na forma padrão da equação do cone elíptico, pois temos uma variável com grau 2 de um lado da equação e do outro temos variáveis de grau 2 com sinais iguais.
O eixo do cone será o eixo (variável “separada”). Figura i)
Resposta
- Cone circular, figura iv)
- Parabolóide Hiperbólico, figura ii)
- Parabolóide Elíptico, figura v)
- Parabolóide Elíptico, figura iii)
- Cone Elíptico, figura i)