Sejam as superfícies dadas pelas equações implícitas
e seja a região limitada pelas superfícies e que contém a origem.
a) Faça o esboço da regição
b) Calculea seguinte integral tripla:
Passo 1
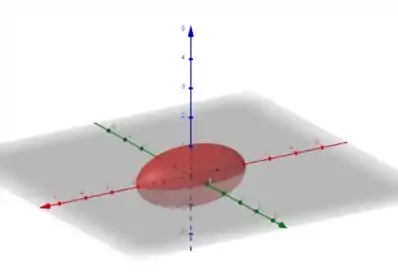
A equação tem a cara de um elipsoide
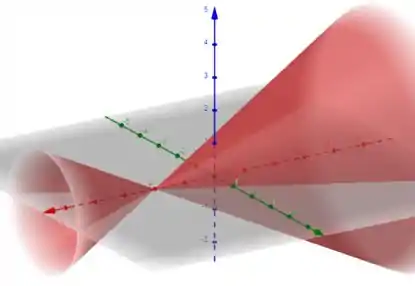
A equação é um cone
Passo 2
Agora que já temos uma noção de onde elas estão, precisamos encontrar onde elas se interceptam.
Na primeira equação podemos isolar
E substituir na segunda, tendo assim:
Abrindo o termo da esquerda
ou
Substituindo na primeira equação:
Para :
Para :
Que é uma circunferência de raio 1 centrada na origem e paralela ao plano
Passo 3
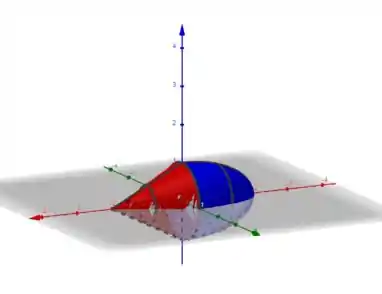
Como é pedido a região limitada pelas superfícies e que contém a origem, ficamos somente com essa região aqui:
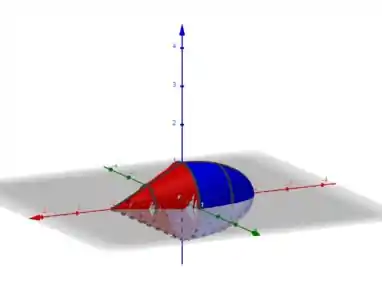
Resposta
Exercícios de Livros Relacionados
Os Exercícios 45-48 fornecem equações para parábolas e nos dize quantas unidades para cima ou para baixo e para direita ou para esquerda cada parábola deve ser deslocada. Encontre uma equação para a n
Os Exercícios 45-48 fornecem equações para parábolas e nos dize quantas unidades para cima ou para baixo e para direita ou para esquerda cada parábola deve ser deslocada. Encontre uma equação para a n
Os Exercícios 45-48 fornecem equações para parábolas e nos dize quantas unidades para cima ou para baixo e para direita ou para esquerda cada parábola deve ser deslocada. Encontre uma equação para a n
A parábola y2 = 8x é deslocada 2 unidades para baixo e 1 unidade para a direita para gerar a parábola (y + 2)2 = 8(x - 1). a. Encontre o vértice, foco e diretriz da nova parábola.b. Represente grafica
A parábola X2 = -4y é deslocada 1 unidades para esquerda e 3 unidade para cima para gerar a parábola (x+1)=4(y-3) a. Encontre o vértice, foco e diretriz da nova parábola.b. Represente graficamente os