Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cone e Parabolóides

Ver Teoria
Exercício 51234678910111213141516171819202122232425

Enunciado

Considere a quádrica a seguir:

x 2 + 5 y 2 = 8 z 2

Identifique a quádrica, encontre os traços, determine as seções e esboce seu gráfico.

Passo 1

Podemos ajeitar a equação da quádrica para ficar na seguinte forma:

x 2 40 + y 2 8 = z 2 5

Que é a equação do cone elíptico.

Passo 2

Vamos agora determinar os traços:

  • Plano x y   ( z = 0 ) :

    • x 2 40 + y 2 8 = 0

    É o ponto 0 , 0,0

  • Plano y z   ( x = 0 ) :

    • y 2 8 = z 2 5

    z = ± 5 8 y

    Temos um par de retas.

  • Plano x z   ( y = 0 ) :

x 2 40 = z 2 5

z = ± 1 8 x

Também temos um par de retas.

Passo 3

Vamos determinar seções paralelas aos planos coordenados.

Interseções:

  • Plano z = k

    • x 2 40 + y 2 8 = k 2 5

    Se k ≠ 0 :

    x 2 40 ( k 2 5 ) + y 2 8 ( k 2 5 ) = 1

    São elipses para k ∈ R   ,   k   ≠ 0

  • Plano y = k

    • x 2 40 + k 2 8 = z 2 5 → x 2 40 - z 2 5 = - k 2 8

    Se k ≠ 0

    x 2 40 ( - k 2 8 ) - z 2 5 ( - k 2 8 ) = 1

    São Hipérboles para k ∈ R   ,   k   ≠ 0

  • Plano x = k

k 2 40 + y 2 8 = z 2 5 → y 2 8 - z 2 5 = - k 2 40

Se k ≠ 0 :

y 2 8 ( - k 2 40 ) - z 2 5 ( - k 2 40 ) = 1

São Hipérboles para k ∈ R   ,   k   ≠ 0

Passo 4

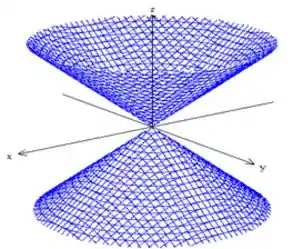
Primeiramente desenhe os traços que a gente achou. Após isso, perceba que as interseções com planos paralelos ao eixo z são elipses. Logo,para representar isso, desenhe duas elipses: uma no topo e outra na parte inferior. O gráfico fica:

Resposta

A quádrica é um cone elíptico . Ela tem os seguintes traços: o ponto ( 0,0 , 0 ) no plano x y , retas z = ± 5 8 y no plano y z e retas z = ± 1 8 x no plano x z .

As interseções com planos k paralelos aos eixos coordenados , com k ≠ 0 , são: No plano z = k temos elipses, e nos plnos x = k e y = k temos hipérboles.

O gráfico fica:

Exercícios de Livros Relacionados

Os Exercícios 45-48 fornecem equações para parábolas e nos dize quantas unidades para cima ou para baixo e para direita ou para esquerda cada parábola deve ser deslocada. Encontre uma equação para a n
Os Exercícios 45-48 fornecem equações para parábolas e nos dize quantas unidades para cima ou para baixo e para direita ou para esquerda cada parábola deve ser deslocada. Encontre uma equação para a n
Os Exercícios 45-48 fornecem equações para parábolas e nos dize quantas unidades para cima ou para baixo e para direita ou para esquerda cada parábola deve ser deslocada. Encontre uma equação para a n
A parábola y2 = 8x é deslocada 2 unidades para baixo e 1 unidade para a direita para gerar a parábola (y + 2)2 = 8(x - 1). a. Encontre o vértice, foco e diretriz da nova parábola.b. Represente grafica
A parábola X2 = -4y é deslocada 1 unidades para esquerda e 3 unidade para cima para gerar a parábola (x+1)=4(y-3) a. Encontre o vértice, foco e diretriz da nova parábola.b. Represente graficamente os