Exercícios de Elevando Matrizes a Expoentes Reais - Lista de Exercícios Resolvida
Questão 5
Se (1,1) e (2,1) são autovetores de A associados aos autovalores 2 e -1, respectivamente, calcule .
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
Questão 6
Considere a matriz e o vetor . Qual é a direção aproximada do vetor ?
A direção do vetor
A direção do vetor
A direção do vetor
A direção do vetor
Ver solução completaQuestão 7
Se , e são os autovalores de uma matriz , então os autovalores de são:
Ver solução completa
Questão 8
Considere o plano em que passa pela origem de equação cartesiana
e a transformação linear espelhamento (ou reflexão) em relação ao plano Denote por a matriz de E na base canônica.
(a) Considere a base ortonormal de
e o vetor (escrito na base canônica). Determine a segunda coordenada de v na base
(b) Escreva na forma , onde Q é uma matriz ortogonal e D é diagonal.
(c) Determine explicitamente a matriz
Ver solução completaQuestão 9
O conjunto dos cidadãos de um certo país está dividido entre os que reside no país e os que vivem no exterior. Todo ano, 10% da população interna vai morar no estrangeira, e 30% que moram fora migram de volta. A continuar esse fluxo migratório, qual a porcentagem aproximada da população total que estará morando no exterior dentro de 10 anos?
(a) 15%
(b) 10%
(c)
(d)
Ver solução completaQuestão 10
Considere as afirmativas abaixo:
Se é autovalor de então é autovalor de
Se é autovetor de , então é autovetor de
(a) Ambas são falsas
(b) é verdadeira e é falsa
(c)
(d)Ambas são verdadeiras
Ver solução completaQuestão 12
Considere o vetor e a matriz . Calcule
(Dica: não é necessário encontrar o polinômio característico de para calcular os autovalores de )
(a)
(b)
(c)
(d)
Ver solução completaQuestão 13
Seja a transformação linear cuja matriz com respeito à base canônica é dada por .
a) Determine os autovalores de .
b) Determine uma base para cada autoespaço de .
c) Exiba uma base tal que seja diagonal (e exiba essa matriz).
d) Seja , . Determine .
Ver solução completaQuestão 14
Considere a matriz e a base canônica do
- Determine uma base do tal que é diagonal.
- Determine D.
- Escreva a relação entre as matrizes A e D usando matrizes de mudança de base.
- Associe a relação obtida no item (b) com a expressão e mostre que
- Calcule .
Questão 16
Seja uma matriz , cujos autovetores estão nos eixos coordenados. Sabe-se que os autovalores associados e podem ser , ou . Indicar quantas matrizes diferentes podemos obter.
Ver solução completa
Questão 18
Seja o operador linear .
Calcule os autovalores de .
Para cada autovalor encontrado em , encontre uma base para o autoespaço correspondente.
é diagonalizável? Se sim, exiba uma base de tal que a matriz seja diagonal e exiba essa matriz.
Sendo a base canônica de , calcule a potência .
Ver solução completaQuestão 19
Seja uma matriz . Assinale a alternativa FALSA:
Se então os autovalores de só podem ser ou
Se as colunas de são linearmente independentes então zero não é um autovalor de
Se então zero é autovalor de
Se então o único autovalor de é
Ver solução completaQuestão 20
Seja a reflexão ortogonal pelo plano . Os autovalores de são:
, e
, e
, e
, e
Ver solução completaQuestão 22
Seja uma matriz . Sabendo que então os únicos autovalores possíveis de são:
Ver solução completa
Questão 23
Seja Q uma matriz ortogonal
(a) Considere a matriz onde
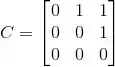
Determine explicitamente
(b) Determine os autovalores da matriz onde
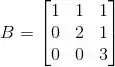
Questão 24
Considere a reta definida por
Seja a tranformação linear que é a reflexão com relação a reta
- Determine
- Seja onde é o plano que contém e é ortogonal à reta Determine
- Determine os autovalores de e os autoespaços associados de cada autovalor.
- Determine uma base de tal que seja diagonal.
- é ortogonalmente diagonalizável? Se sua resposta foi afirmativa, diagonalize ortogonalmente. Se sua resposta foi negativa, justifique.
- Determine
- Determine uma base de
- Determine explicitamente as matrizes e onde é a matriz de na base canônica.