UERJ, Sem Campus, Física I, Provas de Física 1 - UERJ - Primeira Prova, Questão 4a
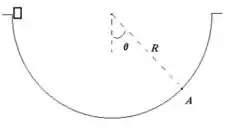
4. Considere uma vasilha semiesférica de raio (conforme a figura acima à direita). Um cubo de gelo de massa cai da borda da vasilha (desconsidere o atrito).
a) Qual o módulo da velocidade do cubo de gelo quando ele passa pelo fundo da vasilha?
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nessa questão a situação é a seguinte: temos uma vasilha semiesférica de raio e na borda dessa vasilha cai um cubo de gelo de massa . Com isso, queremos saber qual é a velocidade do cubo assim que ele passa pelo ponto mais baixo da vasilha.
E aí, como vamos fazer isso? 🤔
Nesse caso, podemos usar a lei de conservação de energia. Como não há atrito do gelo com a vasilha, a energia se conservará em todos os instantes.
Isso quer dizer que toda a energia gravitacional do cubo no momento em que ele está na borda é convertida para energia cinética.
Sacou? Bora começar! 😎
Passo 2
A energia gravitacional é dada por
Onde é a massa do objeto, a aceleração gravitacional e a altura até o ponto de referência.
No nosso caso, pode ser descrito como o raio , assim a energia inicial do cubo de gelo é dada por
Já no momento que o cubo está no ponto mais baixo da vasilha, não há mais altura , porém toda energia foi transformada em energia cinética, que podemos calcular como
Assim, como as duas energias são iguais, podemos igualar as duas equações
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
