USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte I - Cinemática, Leis de Newton, Trabalho e Energia, Questão 68c
Uma partícula de massa move-se em uma trajetória retilínea sob a ação de uma força conservativa , onde é medido em metros e em Newtons.
c) É possível essa partícula ter uma energia mecânica total igual a ? Justifique.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado nos deu uma partícula de massa , que se move na direção por meio da força . A partir disso, nós precisamos determinar se é possível que essa partícula tenha uma energia mecânica total igual a .
Pra isso, vamos precisar do gráfico de que nós construímos no item (b):
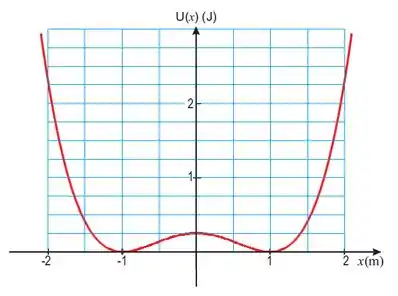
A partir dele vamos conseguir avaliar os valores da energia potencial, cinética e a energia total do sistema, sempre considerando que ela se conserva.
Vamos lá!
Passo 2
Olhando o gráfico do passo anterior, vemos que , a partícula poderá ter movimento oscilatório, que pode ser ao redor da posição ou ao redor da posição , que são os mínimos da função. Esses pontos de mínimo, caracterizam um equilíbrio estável, onde a energia cinética é máxima e a energia total se mantém constante.
Se o movimento for ao redor de , os pontos de retorno são e . Se for ao redor de , os pontos de retorno são e . Então, nesses casos, é possível que a partícula tenha uma energia mecânica total igual a .
Para a região com não é possível esta partícula ter energia total , pois isto implicaria em uma energia cinética negativa.
Valeu, galera! Até a próxima! 😉