USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte I - Cinemática, Leis de Newton, Trabalho e Energia, Questão 65d
Uma partícula de massa se move ao longo da direção sob o efeito da força .
d) Para que valores da energia mecânica total a partícula poderá apresentar um comportamento oscilatório?
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado nos deu uma partícula de massa , que se move na direção por meio da força . Nós precisamos analisar para quais valores da energia mecânica total, a partícula apresenta um movimento oscilatório.
O movimento oscilatório ocorre quando a partícula está confinada em um poço de potencial. Ela está confinada quando sua energia total é menor que a energia necessária para que ela ultrapasse a barreira de potencial de qualquer um dos dois lados.
Sabendo disso e usando o gráfico plotado no item (b), vamos analisar os pontos críticos da função e determinar um intervalo onde ocorre o movimento oscilatório.
Vamos lá!
Passo 2
Vamos dar uma olhada no gráfico do item (b):
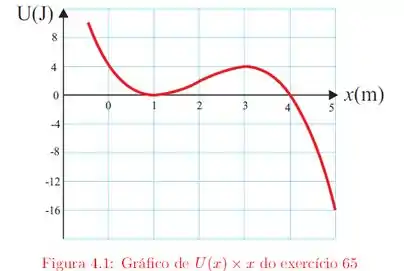
Nós vimos que o movimento oscilatório ocorre quando a partícula está confinada em um poço de potencial. Quando a partícula se aproxima de um dos lados do poço a energia cinética se anula e a energia total é a própria energia potencial naquele ponto.
Para que a energia cinética não seja nula (nem negativa) em nenhum ponto, a energia total deve ser maior que a energia no fundo do poço de potencial, ou seja:
Esse poço de potencial é representado na curva pelo ponto de mínimo em .
O maior valor que a energia total pode atingir para que a partícula possa ainda estar confinada no poço de potencial é o valor máximo da energia potencial. Para encontrar este valor, basta olharmos novamente para o gráfico e verificar os pontos de máximo da função, que nesse caso ocorre para e . Então, temos:
Este é o maior valor de energia para que a partícula esteja confinada no poço de potencial. Assim, para que o movimento seja oscilatório a energia deve ser menor que este valor máximo. Juntando tudo, vamos ter:
Valeu, galera! Até a próxima! 😉