UTFPR - Pato Branco - Física 1 - Listas - Teste 9 - Listas Prof. Marcelo Sandrini - Lista 4 - Questão 16
Durante uma avalanche, uma pedra de desliza a partir do repouso, descendo a encosta de uma montanha que tem de comprimento e de altura. O coeficiente de atrito cinético entre a pedra e a encosta é . Se a energia potencial gravitacional do sistema rocha-Terra é nula na base da montanha, qual é o valor de imediatamente antes de começar a avalanche? Qual é a energia transformada em energia térmica durante a avalanche? Qual é a energia cinética da pedra ao chegar à base da montanha? Qual é a velocidade da pedra nesse instante?
Passo 1
Oiie, tudo bem?
Vamos esquecer tudo isso de avalanche, o que temos aqui é um plano inclinado, e uma partícula que desce pelo plano inclinado. O plano tem um comprimento de e uma altura de . A partícula tem uma massa de e durante sua descida devemos considerar um coeficiente de atrito com o plano de . Assim fica menos confuso não é?
Na alternativa o enunciado nos indica que a base do plano inclinado tem energia potencial nula, isso é uma escolha de referencial que coloca na base, e pede para calcularmos a energia potencial no topo do plano inclinado, ou seja, antes da descida da partícula! Para isso, vamos usar a relação usual
Agora, a pedra começa a descer pelo plano inclinado, como temos atrito parte da energia potencial inicial é transformada em energia cinética e parte se perde como energia térmica. O que precisamos, é analisar qual a quantidade de energia relacionada a cada um. Para isso, é interessante lembrar que a energia térmica liberada é equivalente ao trabalho realizado pela força de atrito, ou seja
Por último, vamos utilizar o restante da energia que não foi liberada para obter a energia cinética e a velocidade com que a pedra chega a base do plano inclinado! Espero que tenha ficado um pouco mais claro! Agora, vem comigo!
Passo 2
Temos o seguinte plano inclinado
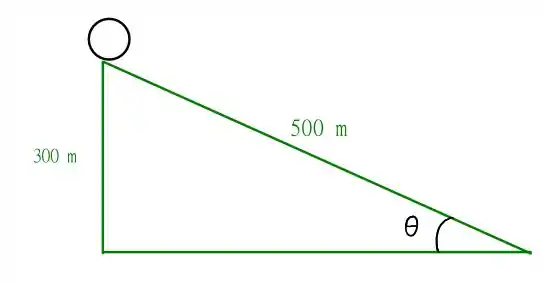
Inicialmente, temos que a pedra está em uma altura , portanto, a energia potencial antes da descida, é dada por
calculando o valor, nos resulta em
A alternativa já foi! Agora precisamos ver quanto desta energia é liberada como energia térmica e o quanto se torna energia cinética! Vem comigo!
Passo 3
Como discutimos no passo 1, temos que a energia liberada termicamente é equivalente a quantidade de trabalho realizado pela força de atrito, ou seja, temos que
Temos que o trabalho realizado pela força de atrito é dado por
em que é o módulo da força de atrito, o comprimento da encosta, e o sinal negativo se dá pois o atrito é sempre contrário ao movimento. Você consegue se lembrar da fórmula para calcular a força de atrito cinético? Ela é da seguinte forma
em que é o módulo da força normal, e , como posto no enunciado. Ou seja, precisamos do módulo da força normal! Como vamos achar isso? Saca só o seguinte esquema
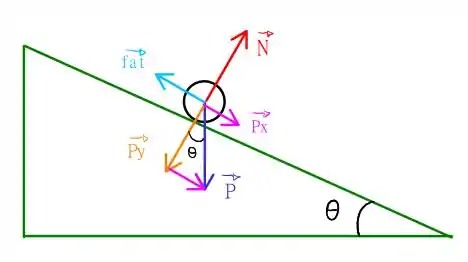
Consegue utilizar este esquema para calcular a força de atrito? Se não, vem cá que a gente dá um jeito!
Passo 4
Como temos que o atrito depende apenas do módulo da força normal, vamos nos preocupar apenas com as forças perpendiculares ao plano. Como não há movimento perpendicular, podemos dizer que
em que é o módulo da componente perpendicular da força peso. Olhando o esquema acima, podemos ver que este componente pode ser obtido fazendo
em que , o módulo do peso da pedra, e podemos obter o ângulo , lembrando que
Ou seja, temos que
De forma que podemos calcular . E a nossa força normal pode ser obtida como
ou seja
e, finalmente, a força de atrito será
Resultando em , que pode ser utilizado para obter o trabalho realizado como
Ou seja, temos que
Maravilha! A nossa segunda alternativa foi! Vamos agora ver quanta energia restou para se transformar em energia cinética! Vem comigo!
Passo 5
Se inicialmente tínhamos uma energia igual a , após a descida o atrito faz com que seja liberada como calor, a energia cinética restante será
E como temos que
Podemos isolar a nossa velocidade para obter
Ou seja, nossa velocidade é tal que
A questão foi isso! te vejo na próxima! Tchau Tchau!