USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte I - Cinemática, Leis de Newton, Trabalho e Energia, Questão 65c
Uma partícula de massa se move ao longo da direção sob o efeito da força .
c) Considere o caso em que a partícula parte da origem com velocidade nula. Discuta o movimento da partícula nesta situação. Qual será a velocidade máxima e em que ponto isso ocorrerá?
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado nos deu uma partícula de massa , que se move na direção por meio da força . A partir disso, nós conseguimos plotar o gráfico da energia potencial no item (b):
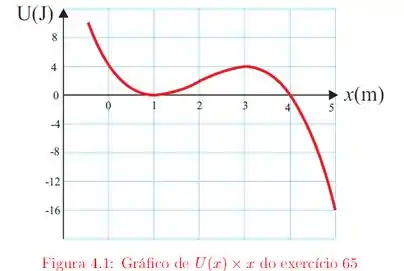
E a partir desse gráfico, nós vamos conseguir analisar o movimento da partícula, que parte da origem com velocidade nula, e descobrir o valor e o ponto de sua velocidade máxima, através do balanço de energia.
Vamos lá!
Passo 2
Derivando e igualando o resultado a zero, nós encontramos os pontos críticos da função em e . Nós vimos no item anterior, que é um ponto de mínimo da função, caracterizado por um equilíbrio estável. E vimos também que o ponto é um ponto de máximo da função, que é caracterizado por um equilíbrio instável.
Além disso, a energia mecânica tem um valor constante dado por:
Ondea energia potencial e a energia cinética são funções da posição da partícula. Então, quando a energia potencial atinge um valor mínimo, de forma a equilibrar a energia do sistema (que é constante), a energia cinética vai ter um valor máximo. Como a energia cinética é dada por:
Onde é a massa da partícula e sua velocidade; dizemos que a velocidade da partícula também é máxima nessa condição. Para o nosso caso, temos um ponto de energia potencial mínima em , certo? Então, é justamente nesse ponto que em que a partícula apresenta velocidade máxima. Pra determinar essa velocidade máxima, a gente precisa conhecer o valor da energia mecância total do sistema.
Passo 3
Assim, como a energia cinética é máxima quando a energia potencial é mínima, o contrário também acontece. Isso quer dizer que nos pontos de máximo de , teremos uma energia cinética mínima. Observe que tem um ponto de máximo em , então, nesse ponto teremos , o que implica em uma velocidade nula também.
Repare que para , . Como a energia mecânica é constante, e , temos . Como esse valor não se altera, no ponto , teremos:
Isso significa que no ponto onde a velocidade é máxima, teremos:
Valeu, galera! Até a próxima! 😉