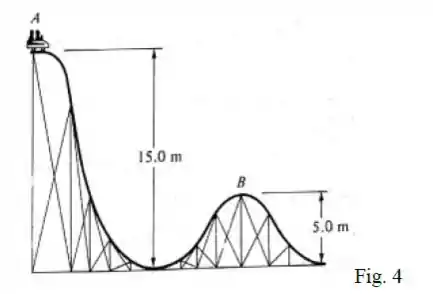
A Figura 4 mostra proposta de uma pista para uma montanha-russa. Cada carrinho partirá do repouso no ponto A e se moverá atrito desprezível. Para evitar que o carrinho saia da pista, qual deve ser valor mínimo para do raio de curvatura no ponto B?

Oi pessoal, tudo bem por aí? Essa questão nos diz que não tem atrito e que precisamos que o carrinho fique na pista!

E agora, como achar o raio de curvatura que faz isso acontecer?

Com conservação de energia! A energia no ponto mais alto vai se transformar em energia cinética e potencial do ponto , e dali vamos conseguir uma informação sobre a velocidade do sistema nesse ponto

Sabemos também que a resultante em um movimento circular é a força centrípeta e que no caso do segundo ponto tem que ser igual ao peso, então é isso! Vamos aplicar a conservação para depois usar a força centrípeta!

Então a ideia é analisar o sinal desse produto com as afirmativas para ver qual delas se encaixa melhor! Beleza?

Bora lá!