USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte I - Cinemática, Leis de Newton, Trabalho e Energia, Questão 68d
Uma partícula de massa move-se em uma trajetória retilínea sob a ação de uma força conservativa , onde é medido em metros e em Newtons.
d) Supondo que a partícula parta da origem com velocidade , encontre a energia mecânica total da partícula. Nesse caso seu movimento é oscilatório? Se sim, encontre os pontos de retorno clássico.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado nos deu uma partícula de massa , que se move na direção por meio da força . A partir disso, nós precisamos determinar a energia mecânica total da partícula, supondo que ela parta da origem com velocidade .
Pra isso, vamos precisar do gráfico de que nós construímos no item (b):
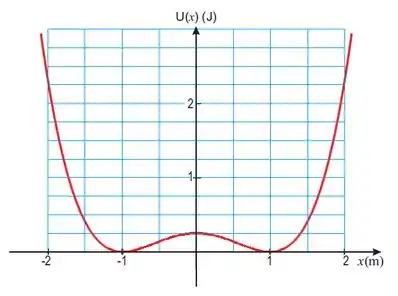
A partir dele vamos conseguir avaliar os valores da energia potencial, cinética e a energia total do sistema, sempre considerando que ela se conserva.
Vamos lá!
Passo 2
Pelo princípio da conservação de energia, temos:
Onde é a energia potencial da partícula e sua energia cinética. Nós queremos encontrar o valor da energia total , que vai ser sempre constante. Pra isso, vamos primeiro tirar do gráfico um valor para a energia potencial, quando . Nesse caso, temos:
Repare que esse é um ponto de máximo da função , como é constante, nesse ponto . De modo análogo, nos pontos de mínimo da função , vamos ter uma energia cinética máxima.
O enunciado nos disse que a partícula parte com velocidade . Então, sua energia cinética nesse ponto vai ser dada por:
Assim, como se conserva em qualquer instante, temos:
Como vimos, temos pontos de mínimo na função que constituem pontos de equilíbrio estável. E em torno de um ponto de equilíbrio estável, a partícula vai apresentar um movimento oscilatório e em alguns pontos a partícula inverte o sentido do movimento. Esses pontos são chamados de pontos de retorno e para a nossa função se encontram em .
Valeu, galera! Até a próxima! 😉