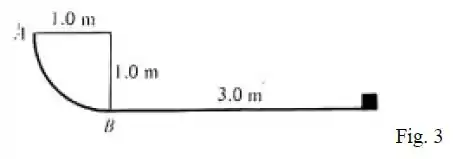
Na Figura, a seção é o quadrante de um círculo de de raio. Um bloco é liberado em e desliza sem atrito até o ponto .
(a) Qual a velocidade do bloco em ?
(b) A parte horizontal não é lisa. Se o bloco para a de , qual é o coeficiente de atrito cinético?
Passo 1
Oi pessoal, tudo bem por aí? Essa questão nos diz que agora o bloco desliza sobre uma superfície co atrito
 pergunta qual é o coeficiente de atrito? Como resolver?
pergunta qual é o coeficiente de atrito? Como resolver?
Do item anterior descobrimos que o corpo chega no chão com velocidade de
e sabemos também que toda essa energia cinética será transformada em atrito, pois sabemos que ele para no fim de percorridos
 então vamos usar o teorema trabalho energia para achar o trabalho da força de atrito! Beleza?
então vamos usar o teorema trabalho energia para achar o trabalho da força de atrito! Beleza?
Bora lá!
Passo 2
Esse teorema diz que
Em termos das velocidades e da força de atrito
O ângulo entre a força e o deslocamento é , pois o atrito sempre apronta no sentido OPOSTO ao movimento. A velocidade final é zero, pois o corpo para.
Tudo bem?

Estamos em um plano horizontal e o movimento é na horizontal, então há equilíbrio de forças nessa direção:
E a força de atrito pode ser escrita em termos da normal
Juntando isso no teorema temos
Simplificando temos
E substituindo
E é isso! Até a próxima!