Exercícios Resolvidos de Energia Potencial Gravitacional

Exercício 28 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 29 30 31 32 33 34 35 36 37 38 39 40 41

Enunciado

UFRJ – FÍSICA 1 – TESTE 03 – Questão 10

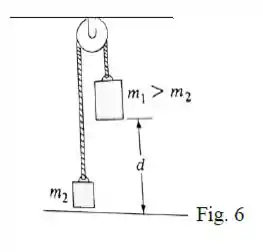
Na Figura 6 se as massas forem liberadas da posição mostrada, encontre uma expressão para a velocidade das massas imediatamente antes que atinja o chão. Use conservação da energia mecânica

Passo 1

Oi pessoal, tudo bem por aí? Essa questão pergunta qual é a velocidade de um corpo quando ele é solto do repouso de uma altura . O problema falou em atrito? Não! Então podemos usar conservação de energia!

v ?

Pela conservação de energia temos que no ponto mais alto temos apenas energia potencial da massa um

E depois? Depois temos energia cinética da massa , da massa (as velocidades adquiridas por elas são iguais! Elas percorrem distâncias iguais em tempos iguais) e temos a energia potencial da massa

E agora?

Agora é só igualar essas formas de energia porque ela foi totalmente transformada!

Então a ideia é juntar essas informações para achar uma expressão para !

Bora lá!

Passo 2

Da conservação

Beleza?

Isolando

Ok?

E é isso! Até a próxima!

Resposta

Exercícios de Livros Relacionados

Uma explosão no nível do solo produz uma cratera com um diâmentro proporcional à raiz cúbica da energia da explosão; uma explosão de 1m e g a t o n de TNT deixa uma cratera de 1k m de diâmetro. Sob o

10. Qual é a velocidade mínima que um disco de hóquei no gelo deve ter para atingir o topo de uma rampa de gelo sem atrito, com 20 ° de inclinação e 3,0m de comprimento?

02. O ponto mais baixo do Vale da Morte, EUA, encontra-se 85m abaixo do nível do mar. O cume do vizinho Monte Whitney tem uma elevação de 4.420m . Qual é a variação de energia potencial de um caminhan

13. Um carro de 1.500k g trafega a 10m / s quando, subitamente, fica sem gasolina próximo do início da descida do vale mostrado na FIGURA EX10.13. Qual será o valor da velocidade do carro quando ele e

11. Um pêndulo é construído amarrando-se uma bola de 500g a um fio de 75c m de comprimento. O pêndulo é deslocado lateralmente em 30 ° e, então, é liberado. a . Qual é o módulo da velocidade da bola n