UTFPR - Pato Branco - Física 1 - Listas - Teste 9 - Listas Prof. Marcelo Sandrini - Lista 4 - Questão 17
Uma criança que pesa desce em um escorrega de que faz um ângulo de com a horizontal. O coeficiente de atrito cinético entre o escorrega e a criança é de . Qual é a energia transformada em energia térmica? Se a criança começa a descida no alto do escorrega com uma velocidade de , qual é sua velocidade ao chegar ao chão?
Passo 1
Oiie, tudo bem?
Aqui temos um problema de plano inclinado! Com uma partícula que pesa , o comprimento do plano inclinado é , e o ângulo com a horizontal é . O plano inclinado é o seguinte
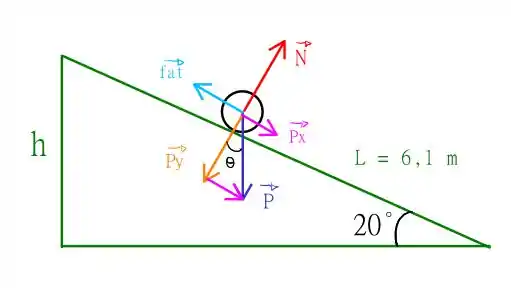
Onde a bolinha é a criança descendo em nosso “escorrega”. O enunciado pede para que calculemos primeiro, a energia térmica liberada devido a força de atrito durante a descida. Alguma ideia de como fazer isso? Nós podemos fazer a seguinte identificação
|
ou seja, a energia térmica liberada é igual ao trabalho realizado pela força de atrito no deslocamento ao longo do escorregador!
A segunda alternativa coloca uma velocidade inicial para a criança no início do escorrega, e portanto, ao chegar à base sua velocidade final será diferente da velocidade final será diferente do que iria ser na situação em que a criança parte do repouso. Mas como fazemos a estimativa desta velocidade?
É necessário lembrar que inicialmente havia uma certa quantidade de energia mecânica (potencial + cinética), a força de atrito elimina parte desta energia na forma de calor, e o restante é transformado em energia cinética durante a descida. Portanto, iremos identificar que a energia cinética final é
em que , é a energia mecânica inicial! Vamos usar isso para resolver a questão! Vem comigo!
Passo 2
Primeiro, vamos calcular a quantidade de energia liberada pela força de atrito, ou seja, vamos calcular o trabalho realizado pela força de atrito, dado por
em que é o módulo da força de atrito, e o sinal de menos vem do fato que o atrito é sempre contrário ao deslocamento. Mas como achar o módulo desta força? Precisamos lembrar que
em que como dado no enunciado, e é o módulo da força normal. No entanto, se observar o esquema no passo 1, é possível identificar que como não há movimento perpendicular ao plano, temos que
Ou seja, temos que , em que é o componente vertical da força peso, que pode ser obtido se analisar novamente o esquema no passo 1, e notar que
Ou seja, temos que , e portanto, temos que
e finalmente, o módulo da força de atrito é dado por
e, o trabalho pode ser identificado como
Ou seja, a energia térmica liberada pode ser identificada como
Uff… Vamos agora analisar a próxima alternativa! Vem comigo!
Passo 3
O criança agora está no topo do escorrega com uma velocidade inicial , e portanto, tem uma energia cinética dada por
a massa da criança é . Portanto, a sua energia cinética é
No entanto, também temos uma energia potencial que é relacionada a altura que a criança está! Ou seja, temos que
Mas qual é o valor de ? Podemos obter lembrando que
Em nosso plano inclinado, dá uma olhada no esquema no passo 1, temos que
Portanto, temos que . E portanto, a energia potencial inicial é dada por
Desta forma, a energia mecânica inicial da criança é
Ótimo! Agora podemos usar esta energia para estimar a energia cinética e final e consequentemente a sua velocidade! Vamos fazer isso!
Passo 4
Da energia mecânica que obtivemos no passo anterior, temos que o atrito fará com que seja liberado na forma de calor, e portanto, restará apenas
Para ser transformado em energia cinética. Identificando então que na base do plano inclinado temos energia potencial nula, podemos escrever que
Isolando então a velocidade, temos que
A questão foi isso! te vejo na próxima! Tchau Tchau!