UFSCAR – Séries e Equações Diferenciais – Simulado 3 – Questão 13
O teorema de existência e unicidade diz que para que um problema de valor inicial da forma , possua solução basta que a função esteja definida em todo plano .
Escolha uma opção:
Verdadeiro ou falso
Passo 1
Fala galera, tudo bem?
O enunciado nos diz que para que um PVI na forma:
Tenha solução é suficiente que a função esteja definida (não tenha indeterminação) em todo plano , isto é, que a função seja contínua para qualquer valor de ou de . Que se possa substituir quaisquer valores de e e que a função vai funcionar, não tenha divisão por zero, raiz de índice par de número negativo, essas coisas...
Vamos verificar se isso é verdade?
Bom, quando falamos em ver se um PVI possui uma ou várias soluções, pensamos no Teorema da Existência e da Unicidade.
Esse teorema nos diz que, se forem satisfeitos todos os passos do teorema, esse PVI tem apenas uma solução. Então para ver se a afirmativa é verdadeira ou não, precisamos ver se o PVI dado satisfaz todas as condições dele.
Certo?
Passo 2
O teorema nos diz o seguinte. Para um PVI na forma:
Precisamos:
- Identificar e calcular
- Verificar onde as funções calculadas no passo 1 são contínuas
- Escolher um intervalo para e outro para onde as funções do passo 1 são contínuas e que contenham a condição inicial
Se conseguir fazer os 3 passos, parabéns, temos que a solução existe e é única!
Tranquilo até aqui?
Passo 3
Se algum desses itens não for satisfeito, então esse PVI pode ou não ter solução, e essa solução pode ou não ser única. Resumindo: se alguma coisa falhar, não podemos dize nada sobre a solução!
Passo 4
Sendo assim, a função ser contínua em qualquer lugar, vai garantir que tenhamos um intervalo que a função é contínua e mais, podemos inserir esse ponto nesse intervalo, já que a função é contínua em todos os lugares.
Mas não é só isso que precisamos. Precisamos que a função seja contínua, sim, mas também que seja contínua, e isso nem sempre ocorre!
Uma função ser contínua não garante que ela tenha derivada, e muito menos que essa derivada seja contínua!
Vamos ver a função módulo de :
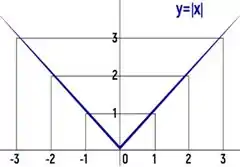
Ela é uma função contínua, não existem buracos nela. Nós conseguimos desenhar ela sem tirar o lápis do papel. Mas essa função não é derivável em , isso porque não temos apenas uma reta tangente que se apoie no gráfico nesse ponto. E se não existe uma reta apenas, a derivada não está definida.
Taí, então se não conseguimos garantir que uma função contínua tenha derivadas contínuas, então falhamos no passo 2 do nosso teorema. Para que a afirmativa do exercício fosse verdadeira, precisávamos que nenhum passo falhasse, o que não ocorreu.
Portanto a afirmativa é falsa.