1c) Na figura abaixo, está representado o gráfico de uma força variável unidimensional que atua sobre uma partícula de massa . Entre as posições e , a força pode ser escrita como , e entre 0 e a força é constante . Seja , , e . A partícula se movimenta no sentido positivo do eixo e no instante que passa pelo ponto sua velocidade é . Calcule a velocidade da partícula quando ela chega na posição . (Você deve incialmente encontrar para fazer a questão!).
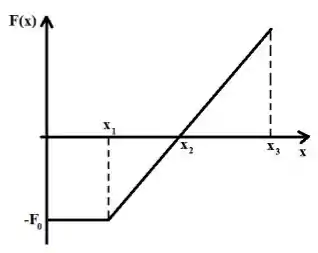
Passo 1
Para o calculo da constante observamos que:
Pela fórmula da força elástica temos que:
Onde o inicial é o de equilíbrio, ou seja, onde a força é nula, que é o . Então:
A velocidade na posição pode ser calculada através do teorema trabalho-energia:
O trabalho total é a área da curva, que pode ser dividida em um retângula e dois triângulos:
Onde, pela fórmula da força elástica:
Substituindo na área:
Assim, substituindo os dados:
Substituindo no teorema trabalho energia: