Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Força Elástica

Ver Teoria
Exercício 111234567891012131415161718192021222324252627282930

Enunciado

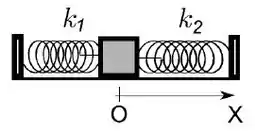
Um bloco de massa m que pode se movimentar sem atrito sobre uma superfície horizontal está preso por duas molas de constantes elásticas k 1 e k 2 , como é mostrado na figura para a situação em que ele se encontra em equilíbrio. Ao ser deslocado de uma distância + x e posteriormente liberado passam a atuar no bloco as forças F → 1 e F → 2 devido às molas. Indique qual das afirmações está correta em relação à força resultante que atuará no bloco.: ( ı ^ é o vetor unitário na direção horizontal OX):

(a) A força resultante será F → R = k 1 + k 2 x ı ^

(b) A força resultante será F → R = - k 2 - k 1 x ı ^

(c) A força resultante será F → R = ( k 1 k 2 ) / ( k 1 + k 2 ) x i ̂

(d) F → 1 + F → 2 = 0 →

(e) F → 1 - F → 2 = 0 →

(f) A força resultante será F → R = - k 1 + k 2 x ı ^

(g) A força resultante será F → R = - k 1 - k 2 x ı ^

Passo 1

Quando o bloco é deslocado no sentido positivo de x (para direita), ele está esticando a mola 1 e comprimindo a mola 2.

Assim, o digrama de forças sobre ele será:

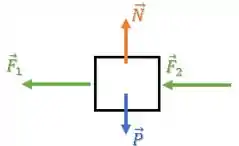
As forças peso e normal se cancelam na vertical.

Assim, a força resultante será:

F R = F 1 + F 2

Passo 2

O módulo da força elástica é dado por:

F e l = k x

Então, temos:

F R = k 1 x + k 2 x

F R = k 1 + k 2 x

Passo 3

Para terminar, queremos o vetor força resultante F → R , ou seja, precisamos dar a direção e sentido desse vetor.

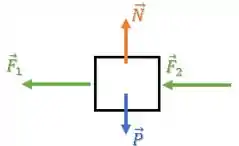
Como a direção positiva do eixo x está para a direita, temos que a força resultante terá uma componente i ^ (direção de x ) negativa:

F → R = - k 1 + k 2 x   i ^

Ficamos com a letra (f).

Resposta

Letra (f)

Exercícios de Livros Relacionados

Os dois cabos que predem os blocos vistos na Figura 5.19 resistem a uma tensão máxima igual a 1,5m g . O bloco de baixo é repentinamente abandonado, de forma que ao se completar a queda permitida pelo
Um distribuidor de bandejas de cafeteria suporta uma pilha de bandejas em uma prateleira pendurada por quatro molas espirais idênticas sob tensão, uma perto de cada canto da prateleira. Cada bandeja é
O sistema da figura está em equilíbrio. A distância d é de 1m e o comprimento relaxado de cada uma das duas molas iguais é de 0,5 m. A massa m de 1 Kg faz descer o ponto P de uma distância h=15 cm. A
Na figura, as molas M 1eM 2 têm massa desprezível, o mesmo comprimento relaxado I 0 e constantes de mola k 1ek 2 ,respectivamente. Mostre que se pode substituir o par de molas por uma mola única equiv
A lei de Hooke descreve uma mola leve com comprimento 35,0c m quando não distendida. Quando uma extremidade é presa ao topo de um batente de porta e um corpo de 7,50k g é pendurado na outra extremidad