Dois blocos e , de massa e respectivamente, estão apoiados em um plano inclinado sem atrito. Eles estão presos entre si por um fio, enquanto o bloco é mantido em repouso por estar preso a parede por uma mola, tendo sua constante elástica igual a . Determine O valor da força de tração no fio e o valor da deformação da mola.
Passo 1
Os dados do problema são
Em problemas literais é sempre bom escrever os dados separados para mais tarde conferir se as respostas estão de acordo com esses dados.
Antes de fazer o DCL de cada bloco, vamos fazer algo que facilita nossas contas, o DCL do sistema. Considerando e uma coisa só.
Vamos responder as perguntas do passo a passo para colocar as forças
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
Sim, ele tem massa.
Sim, o sistema está apoiado no chão.
Não, não existe fio atuando.
Sim, temos uma mola.
O DCL do sistema fica
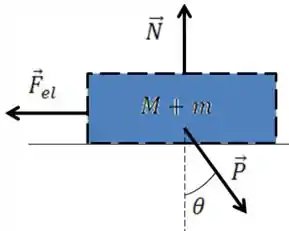
Assim, é mais fácil considerarmos a horizontal e vertical em relação à superfície inclinada, isso facilita nossas contas porque ele não tem movimento vertical em relação a essa superfície.
Passo 2
Como o sistema está em repouso, temos equilíbro em ambos os eixos. Estamos procurando a deformação da mola, então vamos usar o por ele conter a força elástica.
Devemos encontrar usando a “regra do COlado, SEparado”.
Passo 3
Para encontrar a força de tração, precisamos apenas fazer o DCL de um dos blocos, iremos fazer do bloco , respondendo as perguntas do passo a passo
Vamos responder as perguntas do passo a passo para colocar as forças
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
Sim, ele tem massa.
Sim, o sistema está apoiado no chão.
Sim, existe um fio.
Não, não existe uma mola atuando.
O seu DCL fica
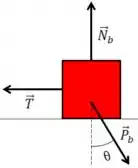
O ângulo fica na força peso com a vertical
O bloco está em equilíbrio, então faremos o equilíbrio no , porque é nele onde está a força de tração.
Devemos encontrar usando a “regra do COlado, SEparado”.