Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Força Elástica

Ver Teoria
Exercício 131234567891011121415161718192021222324252627282930

Enunciado

UFRJ, Física 1, Prova 1, 2016.1

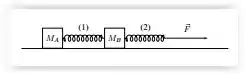
Dois blocos A e B, de massas MA = 3 kg e MB = 7 kg, estão apoiados sobre um plano horizontal sem atrito. Entre os corpos A e B, há uma mola ideal (1) de massa desprezível, e uma outra mola (2), idêntica a esta, se encontra presa ao outro lado do bloco de massa MB, como mostra a figura. Uma força F → constante horizontal é aplicada sobre a mola (2) puxando o conjunto para a direita de modo que os dois blocos se movem com a mesma aceleração. Sendo x 1 e x 2 as deformações das molas (1) e (2), respectivamente, é correto afirmar que:

  1. x 1 = 3 10 x 2
  2. x 1 = 2 x 2
  3. x 1 = x 2
  4. x 1 = 7 10 x 2
  5. x 1 = 0

Passo 1

Vamos primeiro aplicar a segunda lei de newton.

Vamos chamar de F 1 a força elástica em (1) e F 2 a força elástica em (2).

Assim na situação 1 (bloco A), temos:

F 1 = m a a

Na situação 2 (bloco B), temos:

F 2 - F 1 = m b a

Somando as duas chegamos em:

F 2 = a m b + m a

Passo 2

Agora podemos fazer a relação entre as duas forças:

F 2 F 1 = ( m b + m a ) m a    

Sabemos que a força elástica é dada por

F e l = k x

Como a mola é igual para as duas forças, a constante k é igual para as duas:

F 2 F 1 = m a + m b m a = - K x 2 - K x 1 = K x 2 K x 1

m a + m b m a = x 2 x 1

Substituindo os valores de massa, chegamos a:

x 2 x 1 = 10 3

x 1 = 3 10 x 2

Resposta

  1. x 1 = 3 10 x 2

Exercícios de Livros Relacionados

Os dois cabos que predem os blocos vistos na Figura 5.19 resistem a uma tensão máxima igual a 1,5m g . O bloco de baixo é repentinamente abandonado, de forma que ao se completar a queda permitida pelo
Um distribuidor de bandejas de cafeteria suporta uma pilha de bandejas em uma prateleira pendurada por quatro molas espirais idênticas sob tensão, uma perto de cada canto da prateleira. Cada bandeja é
O sistema da figura está em equilíbrio. A distância d é de 1m e o comprimento relaxado de cada uma das duas molas iguais é de 0,5 m. A massa m de 1 Kg faz descer o ponto P de uma distância h=15 cm. A
Na figura, as molas M 1eM 2 têm massa desprezível, o mesmo comprimento relaxado I 0 e constantes de mola k 1ek 2 ,respectivamente. Mostre que se pode substituir o par de molas por uma mola única equiv
A lei de Hooke descreve uma mola leve com comprimento 35,0c m quando não distendida. Quando uma extremidade é presa ao topo de um batente de porta e um corpo de 7,50k g é pendurado na outra extremidad