Exercícios Resolvidos de Força Elástica

Exercício 3 1 2 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

Enunciado

Para a verificação experimental das leis da Dinâmica, foi montado o sistema a seguir:

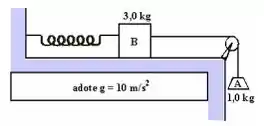
Nele, o atrito é desprezado, o fio e a aceleração são ideais. Os corpos A e B encontram-se em equilíbrio quando a mola “ultraleve” M está distendida de . A constante elástica dessa mola é:

Passo 1

Foi dito que o sistema está em equilíbrio, portanto, a resultante das forças que agem nos dois corpos são necessariamente nulas, segundo a primeira lei de Newton.

Começemos então fazendo o diagrama de corpo livre do peso pendurado A:

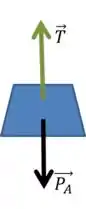
Como a resultante tem que ser zero:

Sabemos o valor de , portanto:

Passo 2

Já para o bloco B, temos:

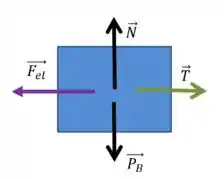
Apesar de existir, o equilíbrio do bloco na direção do eixo não é interessante para nós, já que não nos trará nenhum resultado relevante. Portanto, vamos analisar somente o equilíbrio na direção do eixo :

Como sabemos, a tensão é a mesma para um mesmo fio, portanto:

Aprendemos pela lei de Hook que:

O valor de foi dado, ele é a distensão da mola e vale , portanto, juntando as duas equações, temos:

E chegamos então à resposta:

Resposta

Alternativa B

Exercícios de Livros Relacionados

Os dois cabos que predem os blocos vistos na Figura 5.19 resistem a uma tensão máxima igual a 1,5m g . O bloco de baixo é repentinamente abandonado, de forma que ao se completar a queda permitida pelo

Um distribuidor de bandejas de cafeteria suporta uma pilha de bandejas em uma prateleira pendurada por quatro molas espirais idênticas sob tensão, uma perto de cada canto da prateleira. Cada bandeja é

O sistema da figura está em equilíbrio. A distância d é de 1m e o comprimento relaxado de cada uma das duas molas iguais é de 0,5 m. A massa m de 1 Kg faz descer o ponto P de uma distância h=15 cm. A

Na figura, as molas M 1eM 2 têm massa desprezível, o mesmo comprimento relaxado I 0 e constantes de mola k 1ek 2 ,respectivamente. Mostre que se pode substituir o par de molas por uma mola única equiv

A lei de Hooke descreve uma mola leve com comprimento 35,0c m quando não distendida. Quando uma extremidade é presa ao topo de um batente de porta e um corpo de 7,50k g é pendurado na outra extremidad