Em um bungee jumping, um elástico bastante comprido é amarrado aos pés de uma pessoa, que salta de uma plataforma e cai livremente até ser sustentado pelo elástico. Considere um elástico de tamanho e constante de elasticidade . Despreze a resistência do ar.
a) Desenhe um diagrama de forças que agem sobre a pessoa durante a queda;
b) Faça um gráfico da força resultante atuando na pessoa em função da distância à plataforma de salto;
c) Calcule a distância até a plataforma de salto em que a velocidade de queda é máxima;
d) Encontre a distância até a plataforma de salto em que a velocidade se anula.
Passo 1
a)
Essa é fácil, só tem a força peso e a força elástica do elástico.

Passo 2
b)
A força que atua no bob esponja no inicio da queda é apenas a força peso. A força elástica só vai atuar no bob esponja quando o elástico estiver esticado, ou seja, quando passar do seu comprimento natural .
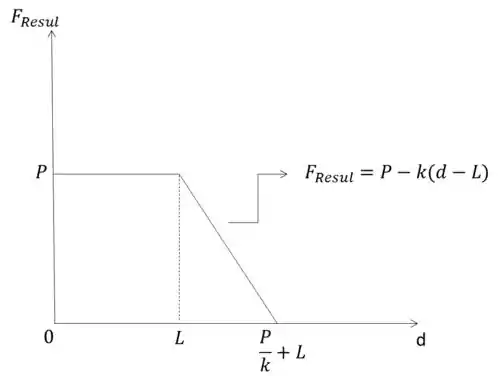
Passo 3
c)
A força elástica vai aumentar cada vez mais com a distância até que chegue um momento em que seu módulo seja igual a força peso. Ou seja, a força resultante será nula. A partir desse momento, a força elástica continuará aumentando, o que acarretará numa força resultante negativa, ou seja, uma desaceleração. Portanto, a velocidade máxima será quando a força resultante se anular.
Passo 4
d)
Por conservação de energia, se a energia cinética é nula, então a energia potencial gravitacional foi convertida “totalmente” em elástica:
Aplicando bhaskara:
Como distância é sempre positivo, vamos considerar só a raiz positiva para não correr risco da distância dar negativa:
Resposta
a)

b)
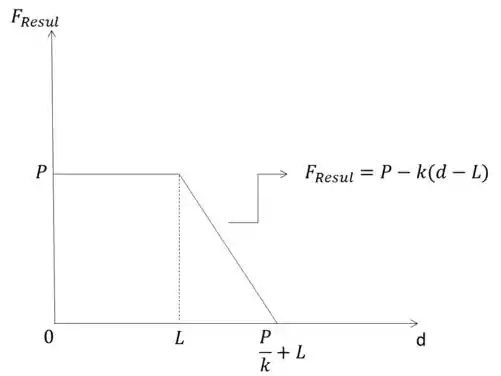
c)
d)