Um bloco de massa encontra-se no chão, preso a uma mola, que tem sua outra extremidade presa a uma parede vertical. O bloco é liberado quando a mola encontra-se distendida e segue um movimento horizontal. Sabendo que não há atrito entre o bloco e o chão, sobre o movimento do bloco é correto afirmar que:
(a) A velocidade do bloco é nula quando a aceleração é máxima.
(b) A velocidade do bloco nunca é nula.
(c) A aceleração do bloco nunca é nula.
(d) A velocidade e aceleração do bloco se anulam nos mesmos instantes.
(e) A velocidade do bloco é máxima nos pontos de inversão do movimento do bloco.
(f) A velocidade do bloco é nula no ponto em que a mola está no seu comprimento natural.
Passo 1
A situação é a seguinte, temos um bloco preso a uma mola e como não há atrito, ele fica oscilando de um lado para o outro:
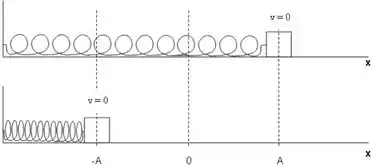
Vamos olhar cada uma das afirmativas.
Passo 2
Começando pela (b).
(b) A velocidade do bloco nunca é nula.
Essa afirmativa é falsa! A velocidade do bloco é nula nas extremidades do movimento.
Ou seja, se o bloco estiver com uma velocidade para positivo (da esquerda para a direita):
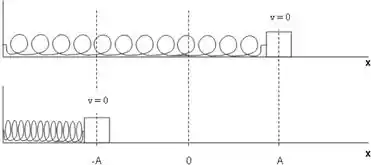
Entre e , a força elástica vai atuar contrária ao movimento, fazendo com que a velocidade do corpo diminua.
Isso vai acontecer até que a velocidade do corpo chegue a zero no ponto , após isso, há uma inversão no sentido e o corpo passa a acelerar no sentido negativo de .
Passo 3
(c) A aceleração do bloco nunca é nula.
A força elástica é dada por:
Onde é a deformação da mola.
Então, na posição onde a mola está relaxada , não há força elástica atuando sobre o corpo e consequentemente não há aceleração.
OBS: Essa situação é momentânea, apenas naquele instante a aceleração é nula.
A afirmativa (c) é falsa.
Passo 4
(d) A velocidade e aceleração do bloco se anulam nos mesmos instantes.
Isso é falso! Acabamos de ver que a aceleração é nula na posição onde a mola está relaxada .
Enquanto isso, a velocidade se anula nas extremidades do movimento, onde há a troca no sentido do movimento e .
Passo 5
(e) A velocidade do bloco é máxima nos pontos de inversão do movimento do bloco.
(f) A velocidade do bloco é nula no ponto em que a mola está no seu comprimento natural.
Novamente, isso não está correto.
A velocidade do bloco é nula nos pontos de inversão de movimento e .
Passo 6
(a) A velocidade do bloco é nula quando a aceleração é máxima.
A velocidade do bloco se anula nas extremidades, certo (pontos e )?
Mas repara que nesses pontos das extremidades, a deformação da mola é máxima.
Como a força elástica depende da deformação:
Temos que a força terá seu valor máximo e consequentemente a aceleração também terá valor máximo.
A afirmativa (a) é nossa resposta!
Resposta
Letra (a)