Um bloco de massa está parado sobre uma superfície, preso a uma mola presa a uma parede, como mostrado na figura abaixo; A mola tem massa desprezível, constante de mola e comprimento quando não está comprimida. O coeficiente de atrito estático entre o bloco e o chão é , e quando o bloco é colocado na posição , ele permanece em repouso na superfície. Espresse suas respostas em termos de , , , e constantes fundamentais.
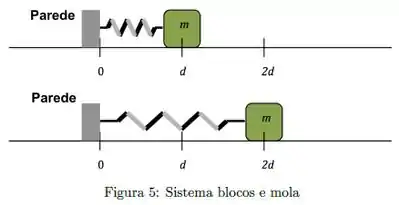
(a) Desenhe o diagrama de forças que agem no bloco quando ele está localizado na posição .
(b) Determine a força de atrito agindo sobre o bloco quando ele esta localizado na posição .
Passo 1
A mola está relaxada quando o bloco se encontra na posição , ou seja, a força elástica é nula nesse ponto.
Mas quando o bloco é deslocado para a posição , a mola começa a esticar e oferecer uma força elástica no sentido contrário (para a esquerda).
Passo 2
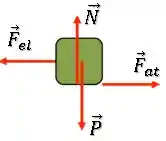
Na letra (a), queremos o diagrama de forças na posição .
A força elástica puxa o bloco para a esquerda, então, a força de atrito está contra essa tendência de deslizamento do bloco e atua para a direita.
Além disso, temos a força peso para baixo e a força normal para cima.
Passo 3
Na letra (b), queremos a força de atrito sobre o bloco na posição .
Devemos tomar um cuidado nessa questão...
Lembra que a força de atrito é dada por:
Muita calma nessa hora.
A força de atrito cinético é dada sempre por essa expressão e usa o coeficiente de atrito cinético:
Já a força de atrito estático, é calculada com essa expressão apenas em seu valor máximo:
Entretanto, ela apresenta valores intermediários enquanto o bloco não atinge a iminência de deslizar.
Okay!
Nessa situação, mesmo que ele tenha fornecido o coeficiente , não podemos garantir que a força de atrito estático é máxima e o bloco está prestes a deslizar...
Passo 4
Então, temos que aplicar a segunda lei de Newton para achar o valor exato dessa força de atrito.
Como o bloco está em equilíbrio, o somatório de forças sobre ele é nulo.
Então, na direção horizontal, temos:
A deformação da mola será :
Então, achamos o valor da força de atrito do bloco para essa situação, mas não podemos dizer que esse é o valor máximo.
Resposta
(a)
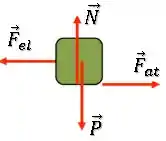
(b)