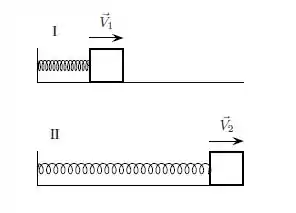
Um bloco, apoiado sobre uma superfície horizontal com atrito não desprezível, está preso a uma das extremidades de uma mola (que tem sua outra extremidade presa à parede), e executa um movimento oscilatório. Na posição representada na Figura I, a mola está comprimida de uma distância em relação ao seu comprimento natural. Em um instante posterior, ela encontra-se na posição representada na Figura II, com a mola distendida da mesma distância . Em ambas as situações o bloco está se movendo para a direita, com velocidades respectivamente iguais a e . Sendo e as forças exercidas pela mola sobre o bloco nas situações I e II, respectivamente, é correto afirmar que:
a) aponta para a direita, aponta para a esquerda e
b) aponta para a direita, aponta para a esquerda e
c) e apontam para a direita e
d) e apontam para a esquerda e
e) aponta para a esquerda, aponta para a direita e
f) aponta para a esquerda, aponta para a direita e
Passo 1
Vamos analisar cada uma das situações:
Situação I:
A mola está comprimida de uma distância , ela irá portanto fazer força para voltar ao seu tamanho relaxada e para isso exercerá no bloco uma força para a direita.
Situação II:
Após passar do ponto em que a mola está no tamanho natural, a inércia do bloco faz com que a mola seja distendida e, consequentemente comece a fazer força para voltar ao seu tamanho natural. Esta força portanto age puxando o bloco para a esquerda.
Passo 2
Para fazermos a análise do módulo das velocidades, devemos estar atentos em duas informações do enunciado: a primeira é que a superfície que o bloco está deslizando tem atrito e a segunda é que a situação II acontece em um instante posterior à situação I.
Usando portanto o princípio da conservação da energia mecânica, sabemos que o que difere a energia entre as duas situações é exatamente a energia que foi dissipada pelo atrito entre os dois instantes. Portanto, concluímos que:
Resposta
(a)