Considere um sistema mecânico de massa no regime de amortecimento fraco na presença de uma força externa , cuja curva de ressonância, com , é apresentada na figura:
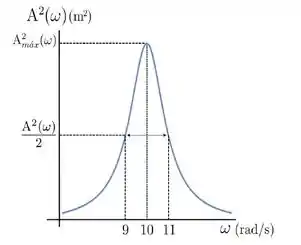
O valor da força externa vale:
(a)
(b)
(c)
(d)
(e)
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado nos deu um sistema mecânico de massa que tá operando no regime de amortecimento fraco na presença de uma força externa. A curva de ressonância é dada na figura e nós precisamos determinar o valor força externa do sistema.
Lembra da amplitude quadrada máxima? Ela é dada por:
Tirando a raiz quadrada dessa equação, temos:
O enunciado nos deu e . Então, pra determinar a força externa só falta saber o valor de e de , certo?
Onde é frequência oscilatória na amplitude máxima e é equivalente a largura de banda . Mas o quê que é largura de banda mesmo?
A largura de banda é a variação da frequência externa oscilatória, quer dizer:
onde e são obtidos através da curva de ressonância . Nós vamos ao gráfico e traçamos uma curva horizontal em . A partir do cruzamento dessa reta com o gráfico, descobrimos, no eixo horizontal, os dois valores de . A diferença desses dois valores nos dá a largura de banda. Olha só:
No nosso caso, o enunciado já marcou a reta horizontal pra gente (o que já ajuda muito), então nós só precisamos extrais os dois valores de , calcular a diferença entre eles para obter . Em seguida, extrair o valor de equivalente a . Assim, substituir os valores na equação , isolando , para obter a força externa do sistema.
Vamos lá!
Passo 2
Vamos dar uma olhadinha no gráfico que a questão nos deu:
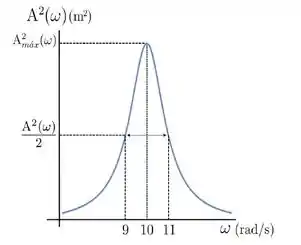
Ele já marcou pra gente a reta horizontal em . Repare que a reta encontra o gráfico em e em . Então, calculando a largura de banda, temos:
Como é equivalente a temos:
Olhando agora para o valor de equivalente a , temos:
Passo 3
Assim, para obter o valor da força externa do sistema, basta usar a equação:
Isolando :
Com , , e , temos:
Que é a nossa alternativa (A).
Valeu, galera! Até a próxima! 😉