Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Força Elástica

Ver Teoria
Exercício 251234567891011121314151617181920212223242627282930

Enunciado

USP, Sem Campus, Física 2, Provas Antigas, P2, 2022, 2

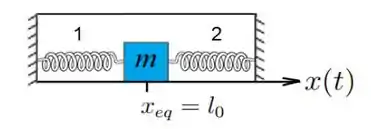
Um bloco de massa m = 2   k g , preso a duas molas idênticas, com comprimentos naturais iguais a l 0 = 0,5   m e constantes elásticas iguais a k = 400   N / m , estão dentro de um recipiente com um líquido, cujo coeficiente de atrito viscoso vale ρ = 80   k g / s . Uma força harmônica de amplitude F 0 = 100   N   e frequência angular ω = 10   r a d / s atua sobre o bloco ao longo da direção horizontal. O atrito entre o bloco e o fundo do recipiente é desprezível. Usando o referencial da figura, determine:

A frequência natural de oscilação, ω 0 , do sistema vale:

(a) ω 0 = 400   r a d / s

(b) ω 0 = 200   r a d / s

(c) ω 0 = 800   r a d / s

(d) ω 0 = 300   r a d / s

(e) ω 0 = 100   r a d / s

Passo 1

Fala, galera! Vamos resolver essa questão!

O enunciado nos deu um arranjo com duas molas que tem comprimentos naturais e constantes el��sticas iguais, essas molas estão presas a um bloco e os três objetos estão dentro de um recipiente com um líquido de atrito viscoso. Então, nós temos uma força harmônica e uma frequência angular que age sobre o bloco e nós queremos determinar a frequência natural de oscilação do sistema.

Lembra como é definida a frequência natural de um sistema? Ela é dada por:

ω 0 = k m

onde k é a constante elástica da mola ou do sistema e m é a massa do sistema, no nosso caso, a massa do bloco.

Como temos um sistema com duas molas, nós precisamos definir uma constante elástica equivalente, que será a soma das constantes elásticas de cada mola. Feito isso, basta a gente substituir o valor de k e de m na equação para encontrar a frequência natural ω 0 .

Vamos lá!

Passo 2

Vamos começar calculando a constante elástica equivalente da mola. Lembra como a gente calcula a constante elástica em uma associação de molas em paralelo? Basta a gente somar a constante de cada mola. Assim, temos:

k e q = k 1 + k 2

Onde k e q é a constante elástica equivalente, k 1 é a constante elástica da mola 1 e k 2 é a constante elástica da mola 2 . Mas o enunciado nos disse que as duas molas são idênticas e tem constantes elásticas iguais a k = 400   N / m . Sendo assim, vamos ter:

k e q = 2 k = 2 ∙ 400 N m

Multiplicando, temos:

k e q = 800   N / m

Passo 3

Agora que temos a constante elástica equivalente k e q = 800   N / m e a massa m = 2   k g , podemos substituir na equação da frequência natural:

ω 0 = k e q m

Substituindo, temos:

ω 0 = 800   2  

ω 0 = 400   r a d / s

Que é a nossa alternativa (A).

Prontinho, galera! Até a próxima! 😉

Resposta

ω 0 = 400   r a d / s

Exercícios de Livros Relacionados

Os dois cabos que predem os blocos vistos na Figura 5.19 resistem a uma tensão máxima igual a 1,5m g . O bloco de baixo é repentinamente abandonado, de forma que ao se completar a queda permitida pelo
Um distribuidor de bandejas de cafeteria suporta uma pilha de bandejas em uma prateleira pendurada por quatro molas espirais idênticas sob tensão, uma perto de cada canto da prateleira. Cada bandeja é
O sistema da figura está em equilíbrio. A distância d é de 1m e o comprimento relaxado de cada uma das duas molas iguais é de 0,5 m. A massa m de 1 Kg faz descer o ponto P de uma distância h=15 cm. A
Na figura, as molas M 1eM 2 têm massa desprezível, o mesmo comprimento relaxado I 0 e constantes de mola k 1ek 2 ,respectivamente. Mostre que se pode substituir o par de molas por uma mola única equiv
A lei de Hooke descreve uma mola leve com comprimento 35,0c m quando não distendida. Quando uma extremidade é presa ao topo de um batente de porta e um corpo de 7,50k g é pendurado na outra extremidad