Classifique as funções abaixo em pares, ímpares ou sem paridade.
- b) c)
Passo 1
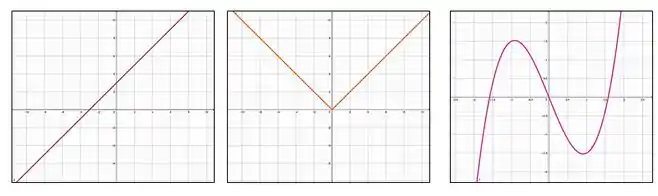
O primeiro com certeza não é nem par e nem ímpar, pois não há simetria nem em relação a y e nem em relação a origem.
- SEM PARIDADE
- PAR
- ÍMPAR
Vamos ao segundo gráfico, observe que ele é simétrico em relação ao eixo y, portanto ele é par.
Por último, o terceiro: Ele será uma função ímpar pois esse gráfico é simétrico em relação a origem.
Agora um obs muito importante: Sempre que possível verifique se sua função é par ou ímpar algebricamente, pois gráficos podem nos enganar, pode parecer que é simétrico quando na verdade não é, beleza?
Resposta
- SEM PARIDADE
- PAR
- ÍMPAR
Exercícios de Livros Relacionados
Faça os gráficos das funções nos Exercícios 37-46. Que simetrias, se houver, possuem os gráficos? Especifiqueos intervalos dentros dos quais a função é crescente e os intervalos em que ela é decrescen
63. (a) Suponha que f e g sejam funções pares. O que você pode dizer sobre f + g e f g ?(b) E se f e g forem ambas ímpares?
a) Se o ponto ( 5 ,3 ) estiver no gráfico de uma função par, que outro ponto também deverá estar no gráfico? b) Se o ponto ( 5 ,3 ) estiver no gráfico de uma função ímpar, que outro ponto também dever
Faça os gráficos das funções nos Exercícios 37-46. Que simetrias, se houver, possuem os gráficos? Especifiqueos intervalos dentros dos quais a função é crescente e os intervalos em que ela é decrescen
Nos Exercícios 47-58, diga se a função é par, ímpar ou nenhuma delas. Jusifique sua resposta.47. f ( x ) = 3