UFES, Cálculo I, Lista 1, 2018.1, questão 43
Nos exercícios 31 a 46 esboce o gráfico da função, especificando o domínio, a imagem e, quando possível, a paridade (par ou ímpar).
43.
Passo 1
Faaaaala, galeeeera! Tudo certinhooo?
Vamos plotar o gráfico desta função. Para desenhar, devemos reescrever a função.
Para isso vamos encontrar suas raízes:
Então nossa função pode ser reescrita como
Passo 2
Nossa função fora do módulo será
Que pode ser escrita de outra forma
Simplificando, temos
Nosso gráfico então será:
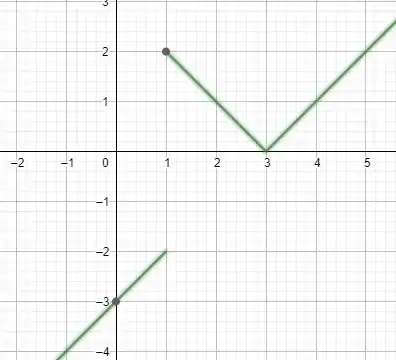
Passo 3
Vamos agora determinar o domínio e a imagem da função dada no enunciado.
Lembre-se que:
Domínio: são os valores possíveis de para esta função;
Imagem: são os valores possíveis de para esta função;
Bom, o domínio desta função será de acordo com o denominador da função, que precisa ser diferente de zero, já que não podemos fazer divisão por zero.
Logo
Já a imagem será os valores de para os quais a função existe
Passo 4
Por fim, vamos verificar a paridade da função.
Uma função será par se:
Uma função será ímpar se:
Vamos verificar na nossa função?
Esta função não obedece às condições acima, pois como podemos observar pelo seu gráfico, esta função não possui simetria em relação a origem. Logo, classificamos como função nem par nem ímpar.
Até mais!
Resposta
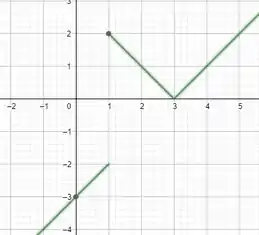
A função não é par nem ímpar