Toda função quadrática é par?
Passo 1
Para mostrarmos que é falso, basta encontrarmos um contra exemplo.
Observe a função quadrática abaixo, dada por
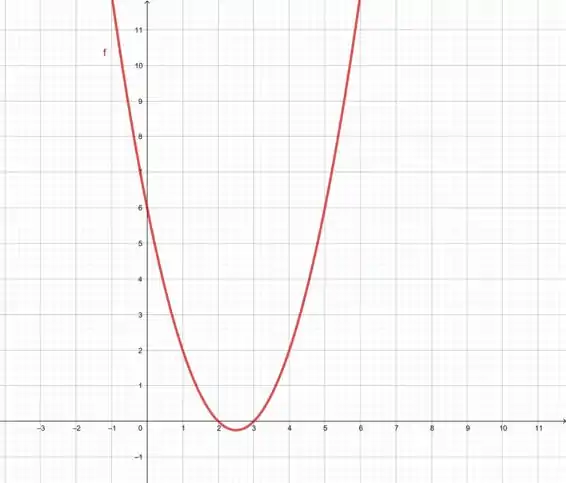
Observe que essa função com certeza não é simétrica em relação ao eixo y.
Mostrando isso algebricamente, temos:
Na real, a nossa função quadrática só será uma função par quando o seu vértice estiver sobre o eixo y. Caso contrário, não.
Portanto, essa afirmativa é FALSA.
Resposta
Falso.
Exercícios de Livros Relacionados
Faça os gráficos das funções nos Exercícios 37-46. Que simetrias, se houver, possuem os gráficos? Especifiqueos intervalos dentros dos quais a função é crescente e os intervalos em que ela é decrescen
63. (a) Suponha que f e g sejam funções pares. O que você pode dizer sobre f + g e f g ?(b) E se f e g forem ambas ímpares?
a) Se o ponto ( 5 ,3 ) estiver no gráfico de uma função par, que outro ponto também deverá estar no gráfico? b) Se o ponto ( 5 ,3 ) estiver no gráfico de uma função ímpar, que outro ponto também dever
Faça os gráficos das funções nos Exercícios 37-46. Que simetrias, se houver, possuem os gráficos? Especifiqueos intervalos dentros dos quais a função é crescente e os intervalos em que ela é decrescen
Nos Exercícios 47-58, diga se a função é par, ímpar ou nenhuma delas. Jusifique sua resposta.47. f ( x ) = 3