UFES, Cálculo I, Lista 1, 2018.1, questão 42
Nos exercícios 31 a 46 esboce o gráfico da função, especificando o domínio, a imagem e, quando possível, a paridade (par ou ímpar).
42.
Passo 1
Faaaaala, galeeeera! Tudo certinhooo?
Primeiramente, vamos reescrever a função para que possamos plotar seu gráfico. Como a raiz está ao quadrado podemos removê-la:
Resolvendo o modulo:
Podemos obter alguns pontos para ajudar a construir o gráfico.
Para :
Logo, o ponto será
Para :
Para :
Como a função que está no modulo é uma parábola, podemos então marcar estes pontos e traçar as semi parábolas.
Nosso gráfico então será:
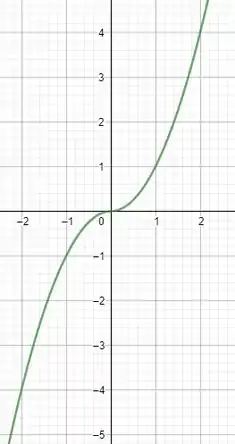
Passo 2
Vamos agora determinar o domínio e a imagem da função dada no enunciado.
Lembre-se que:
Domínio: são os valores possíveis de para esta função;
Imagem: são os valores possíveis de para esta função;
Bom, o domínio desta função são todos os reais. Por que? Isso porque a função modular permite tanto valores positivos quanto negativos como entrada. Podemos colocar qualquer valor real em .
Logo
Já a imagem será todos os valores reais também, pois a função possui correspondência em para todas as possibilidades de entrada.
Passo 3
Por fim, vamos verificar a paridade da função.
Uma função será par se:
Uma função será ímpar se:
Vamos verificar na nossa função?
Substituindo um valor qualquer para , temos:
Então podemos ver que , logo a função é ímpar!
Até mais!
Resposta
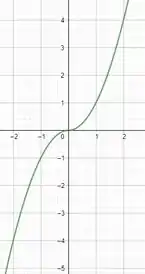
A função é ímpar