P3 de Cálculo 1 da UFRJ - 2020.2

Seja a área da região sob o gráfico , acima do eixo , entre as retas e . Selecione a alternativa que apresenta uma forma correta de obter o valor de como limite de somas de áreas de retângulos.

Sabendo que

Podemos concluir que é igual a

Sobre o limite é correto afirmar que

é

é

existe e é igual a

existe e é igual a

este limite não existe.

Um trapézio é inscrito num circulo de raio , de modo que a base do trapézio é o diâmetro do círculo. Sabendo que o trapézio de área máxima tem área , podemos concluir que a área do disco de raio é

.

.

.

.

.

Selecione a alternativa que fornece a expressão correta para

Selecione a alternativa que representa a expressão correta de .

Seja definida por

Selecione a opção que apresenta os intervalos onde o gráfico da função é côncavo para baixo:

e

e

e

e

Seja

Então é igual a

Uma população de bactérias é de no tempo e sua taxa de crescimento é de bactérias por hora depois de horas. Qual é a população depois de seis horas?

O valor correto de é

Seja . Então, é igual a

A área da região sob o gráfico de função

acima do eixo , entre as retas e , é:

O volume máximo do cilindro circular reto que pode ser inscrito numa esfera de raio é igual a

Uma casa tem uma janela em forma de arco cujo formato é dado pela metade superior de uma elipse. A casa será reformada e deseja-se colocar concreto no arco a fim de fechá-lo, mantendo-se apenas uma janela retangular, como na figura abaixo:

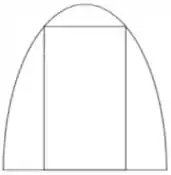
Considerando que o arco original tem altura igual a e largura igual a , qual o maior valor possível para a área dessa janela?

1 Seja uma função contínua no intervalo tal que . Considere

O valor de é

Selecione qual dos pontos abaixo pertence à reta tangente ao gráfico de no ponto , onde

O valor do limite é

.

.

.

.

.

Seja uma função contínua em . Suponha que o gráfico da derivada seja dado pela figura abaixo:

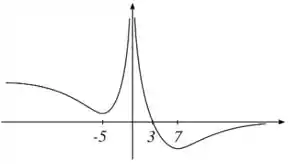
Considere as seguintes afirmações sobre o gráfico de :

é necessariamente um ponto de mínimo local.

é necessariamente um ponto de máximo local.

é necessariamente o valor máximo absoluto.

é necessariamente um ponto de inflexão.

Selecione a alternativa correta:

As afirmações e são verdadeiras e e são falsas

Todas as afirmações são falsas

As afirmações e são verdadeiras e e são falsas

Todas as afirmações são verdadeiras

As afirmações e são verdadeiras e e são falsas

Sejam e números reais tais que . Seja uma função tal que e são funções contínuas para todo . Se

então podemos afirmar que, necessariamente,

é decrescente em .

é crescente em .

existe tal que tem um mínimo local em .

O gráfico de é côncavo para cima em .

existe tal que tem um máximo local em .

Seja . Considere as seguintes afirmações:

A curva não tem assíntotas verticais.

A função tem um máximo local, mas não tem um mínimo local.

A função tem um mínimo local, mas não tem um máximo local.

O gráfico é côncavo para baixo.

O gráfico de tem um único ponto de inflexão.

A respeito das afirmações acima, podemos concluir que

e são verdadeiras, e são falsas.

e são verdadeiras e e são falsas.

e são verdadeiras e e são falsas.

e são verdadeiras e e são falsas.

e são verdadeiras e e são falsas.