UFRJ – Cálculo 1 – 2020.2 – P3 – M.Escolha
Uma casa tem uma janela em forma de arco cujo formato é dado pela metade superior de uma elipse. A casa será reformada e deseja-se colocar concreto no arco a fim de fechá-lo, mantendo-se apenas uma janela retangular, como na figura abaixo:
Considerando que o arco original tem altura igual a e largura igual a , qual o maior valor possível para a área dessa janela?
Passo 1
Vem comigo que a gente detona essa juntos!
Vamos colocar uns eixos na figura para facilitar nossa vida, assim:
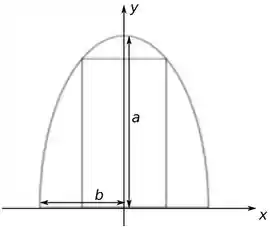
Temos um problema de otimização em mãos, para encontramos a maior área possível da janela temos que relacionar a equação da elipse coma área do retângulo.
E com isso achar uma função da área em função de uma variável, aí a gente deriva essa função e iguala a zero para ver o valor que faz essa área ser máxima.
A equação da elipse considerando que ela esteja centrada na origem, é dada por:
A área do retângulo é dada por:
Passo 2
Vamos isolar na equação da elipse, temos:
Assim temos:
Substituindo isso na expressão da área do retângulo, temos:
Passo 3
Agora vamos derivar essa expressão da área em função de , assim:
Então temos que:
Agora igualando isso a zero, temos:
Esse é o valor de que faz a área ser máxima, então vamos calcular para esse valor de .
Passo 4
A área é dada por:
Substituindo , temos:
Assim temos:
Usando que e , assim:
Então nossa escolha vai ser a letra .