Halliday - Vol. 3 – 9º edição – Capítulo 23 – Seção 4 – Exercício 11
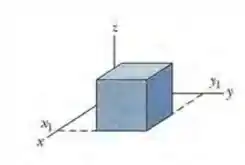
(Capítulo 23.4 – Exercício 11) A Fig. 23-31 mostra uma superfície gaussiana com a forma de um cubo de 2,00 m de aresta, com um vértice no ponto x1 = 5,00 m, y1 = 4,00 m. O cubo está imerso em um campo elétrico dado por, com y em metros. Qual é a carga total contida no cubo?
Passo 1
Oii gente, vamos lá que já estamos ficando craques na Lei de Gauss!
Aqui temos uma superfície gaussiana que é um cubo de lado . Esse cubo tem vértice no ponto . Também sabemos o campo que passa por esse cubo: .
O que precisamos encontrar é a carga total dentro desse cubo, certo? Para fazer isso, utilizamos:
Onde Mas primeiro vamos precisar calcular o fluxo elétrico que passa por esse cubo. Podemos simplificar a conta se levarmos em conta que termos constantes do campo elétrico não contribuem para o fluxo elétrico. A única componente que não tem termos constantes é a componente y, que faria de acordo com .
Então vamos lá calcular o fluxo elétrico para podermos encontrar a carga
Passo 2
Podemos calcular a componente y campo do elétrico para a face direta, Ed, e esquerda, Ee
Como a face esquerda está em :
E como a face direita está em :
Agora, podemos utilizar a seguinte relação:
Onde é a área das faces
Calculando o fluxo:
O sinal negativo no segundo termo vem da direção da normal da área.
Passo 3
Finalmente, podemos utilizar a lei de Gauss para achar a carga:
Sucessooo