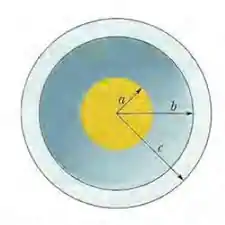
(Capítulo 23.9 – Exercício 49) Na Fig. 23-50, uma esfera maciça de raio é concêntrica com uma casca esférica condutora de raio interno e raio externo . A esfera possui uma carga uniforme e a casca possui uma carga . Determine o módulo do campo elétrico

em ;

em ;

em ;

em ;

em ;

em .

Determine a carga

na superfície interna e

na superfície externa da casca.

a) Precisamos saber que no caso da esfera maciça interna, para uma volume de , e por termos uma carga uniforme podemos aplicar a regra de três para a carga interna de uma esfera de raio com :

Onde é a carga da esfera amarela com um raio de . Então, multiplicando em cruz:

Substituindo o valor da carga interna na fórmula do campo elétrico de uma esfera, então o campo elétrico nessa situação será:

Na letra (a) nos foi dito que , então substituindo nós temos:

De boas??

E para a letra (b) temos que , substituindo na fórmula que achamos:

Sabendo que:

Então:

Preparados para a (c)??

Já a letra (c) nós queremos o campo elétrico para , ou seja o campo elétrico na superfície da esfera de raio . Pela Lei de Gauss, que:

Substituindo o raio:

Então substituindo os valores para encontrar o campo elétrico na superfície da esfera amarela nós temos:

Na letra (d) nós temos um caso diferente, ? A Lei de Gauss já nos disse que:

Só que a carga interna na esfera de raio ainda continua sendo a carga na esfera amarela e que é igual a então:

Nesse caso . Portanto:

Substituindo:

Na letra (e) o caso também é diferente, certo? Agora teremos um !!

Nesse caso, por se tratar de uma casca condutora, a carga negativa da casca esférica que foi completamente atraída para a superfície interna da casca, pela carga positiva de mesmo módulo presente na esfera maciça de raio . Logo não precisamos fazer toda a análise do passo 1. Logo a nossa carga interna dessa região é igual a:

Então o campo elétrico na letra que nos dá será de:

Quando nós temos observamos a mesma situação da anterior.

A carga total dentro da esfera de raio é nula, já que a carga da esfera amarela se anula com a da casca. Então para a letra (f) temos:

E, por isso:

As letras e nos pedem para determinar a carga na superfície interna e externa da nossa casca esférica.

Veja bem, o que acontece com essa casca esférica quando tem aquela esfera carregada concêntrica a ela:

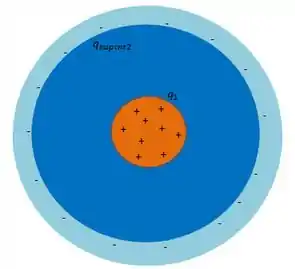
Pelo fenômeno de indução eletrostática, a esfera no centro de carga atrai as cargas de mesmo módulo e sinal diferente da casca esférica para a superfície interna da mesma. Isso só ocorre por que a casca esférica é condutora!

Como a carga líquida será zero:

Portanto, a carga da superfície interna será

Agora, precisamos saber o que acontece com a superfície externa dessa casca esférica!

Como ela é condutora, podemos dizer que toda sua carga estará em suas superfícies, no caso, temos aqui a superfície interna e a externa, sabemos que a interna é negativa e vale , sobre a externa não sabemos nada...

Mas podemos dizer que a carga total apresentada pela casca será:

Substituindo o que temos:

Ufaaa !! Essa foi bem puxada !!

Mas se vocês olharem com muita atenção e carinho vocês vão tirar de letra !!