Halliday - Vol. 3 – 9º edição – Capítulo 23 – Problemas Adicionais – Exercício 76
(Capítulo 23 – Problemas Adicionais – Exercício 76) Um cilindro muito longo de raio R possui uma distribuição volumétrica de cargas uniforme. (a) Mostre que, a uma distância r
Passo 1
Oii gente, tudo belezinha?
Ta pronto pra mais uma? Então bora!
Temos um cilindro longo de raio R com uma distribuição de cargas, para isto vamos fazer uma superfície gaussiana do tipo:
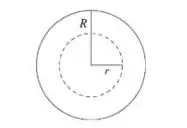
Considere uma superfície gaussiana na forma de um cilindro de raio r e comprimento L, coaxial com o cilindro carregado, representada na figura do item a pela linha tracejada. A carga envolvida pela superfície gaussiana é , na qual é o volume do cilindro.
Nesse exercício, queremos analisar o campo elétrico da situação, pra isso vamos usar a Lei de Gauss e a simetria, vamos lá!
Passo 2
(a) Como, por simetria, o campo elétrico é radial, o fluxo total através do cilindro gaussiano é
E de acordo com a lei de Gauss,
Igualando os dois fluxos:
Isolando :
Show!
Passo 3
(b) Considere uma superfície gaussiana cilíndrica de raio r > R. Se o campo elétrico externo é
, o fluxo através da superfície gaussiana é .
A carga envolvida é a carga total em um segmento do cilindro carregado, de comprimento L, ou seja,. Assim, de acordo com a lei de Gauss,
Arrasamos demais!
Resposta
(a)
(b)