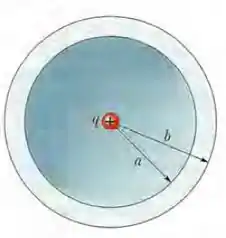
(Capítulo 23.9 – Exercício 51) Na Fig. 23-52, uma casca esférica não condutora com um raio interno e um raio externo possui uma densidade volumétrica uniforme de cargas positivas , onde é uma constante e ré a distância em relação ao centro da casca. Além disso, uma pequena esfera de carga está situada no centro da casca. Qual deve ser o valor de para que o campo elétrico no interior da casca () seja uniforme?

Pela Lei de Gauss, usando uma superfície gaussiana de raio , tal que , a carga interna é dada pela integral , sendo a densidade de carga por unidade de volume. Assim, sendo essa carga, temos:

Além disso, a carga total da superfície gaussiana é dada por:

Como o campo elétrico é radial e o fluxo elétrico dado por , então:

Isolando na expressão anterior, vem:

Agora, o que significa um campo elétrico uniforme?

Significa um campo constante no espaço. Para que a expressão anterior seja constante com , então devemos zerar a parcela :

Substituindo os valores (lembrando que e )

Fazendo isso, encontramos:

Fechou??