Halliday - Vol. 3 – 9º edição – Capítulo 23 – Seção 4 – Exercício 4
(Capítulo 23.4 – Exercício 4) Na Fig. 23-28, uma rede para pegar borboletas está imersa em um campo elétrico uniforme de módulo . O plano do aro da rede, uma circunferência de raio , é mantido perpendicular à direção do campo. A rede é eletricamente neutra. Determine o fluxo elétrico através da rede.
Passo 1
E aíí gente, tudo certinho?
Sabe aquelas redes de caçar borboleta que a gente vê nos desenhos? Nesse exercício, temos uma dessas com raio que ta imersa em um campo elétrico .
E aí o que queremos é determinar o fluxo elétrico através da rede. Vamos fazer um desenho pra visualizar isso.
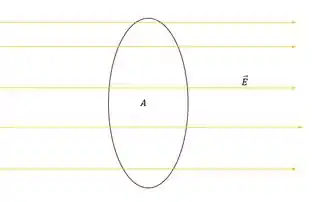
Para calcular o fluxo do campo através da rede é só a gente calcular a área da rede e aplicar a equação do fluxo:
Que podemos escrever como
Onde é o ângulo entre e
Então bora!
Passo 2
Para encontrarmos o ângulo entre os vetores, vamos analisar pra onde aponta o vetor área:
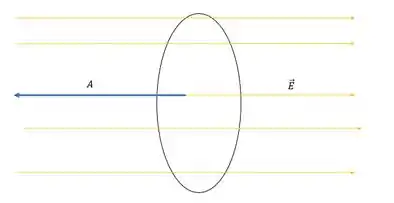
Como a rede tá pra esquerda, o seu vetor área está nesse sentido, portanto podemos dizer aqui que:
Vamos então calcular essa bendita área:
Passo 3
E agora com a área vamos substituir todo mundo na equação do fluxo com
Show!!