Halliday - Vol. 3 – 9º edição – Capítulo 23 – Seção 7 – Exercício 24
(Capítulo 23.7 – Exercício 24) A Fig. 23-36 mostra uma seção de um tubo longo de metal, de paredes finas, com um raio e uma carga por unidade de comprimento . Determine o módulo do campo elétrico a uma distância radial (a) ; (b) . (c) Faça um gráfico de em função de para .
Passo 1
E aeee galera, tudo bem? Vamos lá entender direitinho esse exercício
Temos um tubo de metal com raio e densidade linear de . E aí queremos encontrar o campo elétrico em diferentes situações
A chave pra gente resolver essa questão encontra-se na Lei de Gauss. Segundo ela, existe essa relação entre a integral do campo elétrico ao longo da superfíce (fluxo do campo elétrico) de formato qualquer e a carga interna a ela (sendo a área superficial considerada):
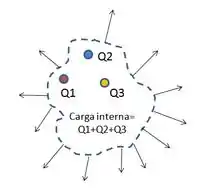
Então vamos lá fazer item por item
Passo 2
No caso da letra (a), a gente considera uma superfície cilíndrica de raio na Lei de Gauss. Mas perceba: a carga interna a essa superfície é zero, pois não há nenhuma entidade carregada no interior dela.
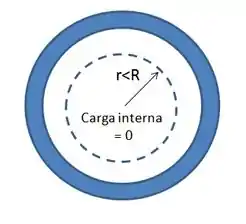
Então, nesse caso, a gente tem que, como :
então:
Passo 3
(b) Agora, na letra b), qual é a carga interna a uma superfície de raio ?
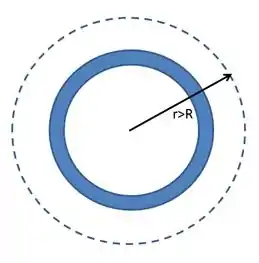
Veja que, nesse caso, dentro da superfície cilíndrica pontilhada (vista de cima) tem um cilindro carregado. Por isso, a carga interna será nula! Como podemos calcular então essa carga?
Repare que a questão nos deu a densidade de carga por unidade de comprimento do cilindro interno. Então, considerando como esse comprimento, temos:
Passo 4
Agora, vamos trabalhar com a superfície externa pontilhada de raio . Pela Lei de Gauss:
Nesse caso, a unidade de área a ser integrada é parecida com a comentada no passo anterior, indicada na figura:
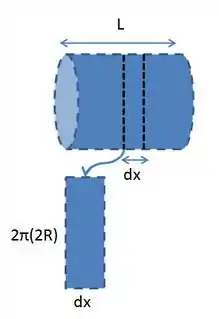
Assim:
Usando essa unidade na integral, a gente fica com essa expressão:
Ou seja:
Substituindo os valores do enunciado nessa equação, temos:
Passo 5
Para colocarmos o campo elétrico num gráfico que o relacione com a distância ao eixo central do cilindro, basta lembrarmos da Lei de Gauss que usamos logo no início.
(I) Como na região em que não há cargas internas a superfície, o campo elétrico é nulo.
(II) Na região em que , o campo elétrico é dado por , pelo que desenvolvemos anteriormente.
Assim, o gráfico nesse caso fica dessa forma:
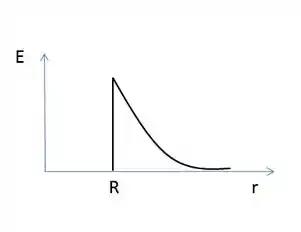
Sucesso?